近接露光とは？
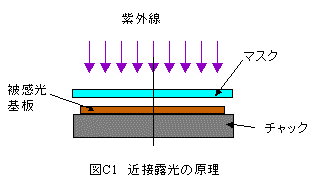
近接露光とは図C1に示すようにマスクと被感光基板の間隔を僅かに設けて、紫外線を 照射することにより、マスクパターンを基板に転写する露光方法のことです。
被感光基板にはレジスト（感光材料）を塗布し、マスクパターンを転写して現像する ことによって、パターンが形成できます。
この方法は、簡単な構成でマスクの損傷を防止できますが解像度が劣化します。 解像度に影響する要因は主にマスクと被感光基板の間隔、露光光照明角度分布、波長等ですが これらの因果関係を理解することは重要です。
近接露光の光強度分布計算の原理
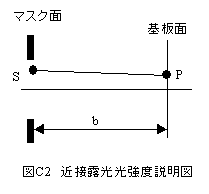
図C2に近接露光の光強度分布計算の原理説明図を示します。
| 記号 | 説明 |
| S | マスク面の任意の位置 |
| P | 基板面の任意の位置 |
| b | マスク面と基板面の間隔 |
| β | 線分SPの長さ-b |
| λ | 波長 |
| σ | マスク面開口部の面積 |
| dσ | S点の微小面積 |
| U0(S) | S点の光の波動 |
| U(P) | P点の光の波動 |
とすると下記C1式でP点の光の波動はあたえられます。
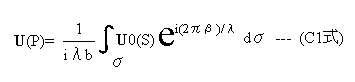
上記式は一見単純そうにみえますが、U0(S)は複素数で与えられる任意の関数であり 、この積分を実行するには工夫が必要です。
U0(S)一定の矩形開口の光強度の計算式
U0(S)一定の矩形開口の場合は計算が容易になります。
| 記号 | ：説明 |
| ξ | ：S点のX方向座標 |
| η | ：S点のY方向座標 |
| ｘ | ：P点のX方向座標 |
| ｙ | ：P点のY方向座標 |
| ξ1 | ：開口のX方向最小位置 |
| ξ2 | ：開口のX方向最大位置 |
| η1 | ：開口のY方向最小位置 |
| η2 | ：開口のY方向最大位置 |
とした場合βは下記式となります。
β=線分SPの長さ-b
={b2+(ξ-ｘ)2+(η-ｙ)2}1/2-b
≒(ξ-ｘ)2/(2b)+(η-ｙ)2/(2b) -----(C2式）
また微少面積dσは下記式となります。
dσ＝dξdη -----(C3式）
矩形開口の波動U0(S)はU0で一定とし、(C1式）に(C2式）(C3式）を代入して整理すると下記式となります。
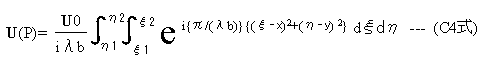
(C4式)は二重の定積分の式でこのまま計算を実行して、矩形開口の波動を求めることができますが、計算しやすいように変数変換を行います。
v={2/(λb)}1/2(ξ-ｘ) -----(C5式）
w={2/(λb)}1/2(η-ｙ) -----(C6式）
変数変換後は下記式となります。
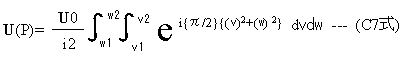
(C5式）(C6式）(C7式）式より任意の点、x,yの波動の振幅を求めることができます。
また光の強さI(P)は、波動振幅の絶対値の自乗として求めることができます。
I(P)＝｜U(P)｜2 -----(C8式）
(C7式）と(C8式）で近接露光における矩形開口パターンの光強度分布を計算できます。
複雑なパターンの光強度の計算
実際のパターンは矩形ではなく、複雑な形状をしています。また場所により透過率が異なったり、光の位相差が異なる場合もあります。
しかし、どのような複雑なパターンも領域を矩形に分割し、矩形パターンの集合で近似できます。
(C7式）は矩形内は均一な光強度と位相差を前提としていますが、矩形パターン間はその制約がありません。そして複雑なパターンの波動Us(P)はU(P)の総和として求めることができます。
Us(P)=U(P) -----(C9式）
(C9式）は(C7式）の結果を単純に総和したものです。これで複雑なパターンの波動を求めることが可能です。そして矩形パターン間は光の強度も位相差も任意に変えることができます。従って数多くの矩形パターンの集合としてパターンを定義すれば複雑なパターンも近似できます。
複雑なパターンの光の強さIs(P)は、波動振幅の絶対値の自乗として求めることができます。
Is(P)＝｜Us(P)｜2 -----(C10式）
(C9式）と(C10式）で近接露光における複雑なパターンの光強度分布を計算できます。
照明光源の傾斜と広がり
以上の説明においては、照明はマスクパターンに垂直に照射する平行光線を前提として、解説しました。しかし、実際の照明は垂直に照射する平行光線ではなく、照明光源の傾斜と広がりを持っています。
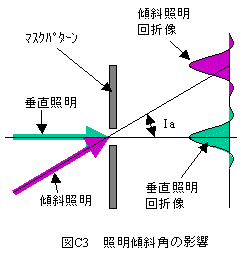
照明の傾斜角の影響関係図を図C3に示します。
図C3に示すようにマスクパターンに傾斜した照明が照射されると回折像の角度は傾斜角度分シフトします。また、回折像の分布は垂直照明と同じで単純に中心角度がシフトします。
もう一つ重要な仮定が必要となります。それは、角度の異なる光が干渉するか？あるいは 干渉しないか？という仮定です。一般的な条件において、角度の異なる照明は干渉しないと仮定します。
この仮定は、光源は無限遠にあり、異なる角度の照明は異なる光源からでたと仮定されます。
異なる光源からの光は時間的に位相がランダムと仮定します。従って、異なる角度の照明は干渉しません。この場合の数学的な処理は、光の波動の和ではなく、光の強度の和として扱います。
俗語かもしてませんが、光の波動の和を「ベクトル和」、光の強度の和を「スカラー和」といって区別します。
すなわち、干渉性の光を扱う場合は「ベクトル和」の処理を行い、非干渉性の光を扱う場合は「スカラー和」の処理を施します。一般に波動光学では、波動の時間項は無視して計算しますが、光の条件によって、 「ベクトル和」と「スカラー和」の使いわけを行います。
では、照明の傾斜角度が連続的に変化する照明光の広がりがある場合は、どうすればよいでしょうか？
実際には、このようなケースがほとんどです。しかし、投影像の光強度分布を計算するにあたって、照明角度を連続として計算することはできません。
複数の傾斜角を持つ照明光の「スカラー和」として投影像の光強度分布を計算します。この場合、照明光線の数を多くすれば誤差が減りますが、計算時間が長くなるためあまり多くもできません。本プログラムでは13本の光線で照明光の広がりを近似しています。
計算の実行
VBAソフト「近接露光.xls」をダブルクリックして起動した後、 シート「デフォルト条件」の条件表の内容をシート「IN_FM」にコピーします。
次にシート「操作」の「計算実行」ボタンを押します。
計算結果の概要が表示されます。
シート「デフォルト条件」の内容は下記表に示す通りです。
| No | 記号 | 値 | 単位 | 説明 |
| 1 | WL | 0.4 | μm | 波長 |
| 2 | F | 100 | μm | マスク面とスクリーン面のギャップ量 |
| 3 | INA | 0.01 | rad | 照明の広がり角度（照明NA) |
| 4 | X1 | -10 | μm | 光強度計算領域のX方向min値 |
| 5 | X2 | 10 | μm | 光強度計算領域のX方向max値 |
| 6 | Nx | 50 | 整数 | 光強度計算領域のX方向分割数(最大140まで) |
| 7 | Y1 | -10 | μm | 光強度計算領域のY方向min値 |
| 8 | Y2 | 10 | μm | 光強度計算領域のY方向max値 |
| 9 | Ny | 50 | 整数 | 光強度計算領域のY方向分割数(最大140まで) |
| 10 | Np | 5 | 整数 | 矩形パターン数を設定(整数最大500まで) |
| No | U0r[i] | U0i[i] | Xmin[i] | Xmax[i] | Ymin[i] | Ymax[i] |
| 1 | 1 | 0 | -10.0124922 | -7.751773991 | -50 | 50 |
| 2 | -1 | 0 | -7.751773991 | -4.473253849 | -50 | 50 |
| 3 | 1 | 0 | -4.473253849 | 4.473253849 | -50 | 50 |
| 4 | -1 | 0 | 4.473253849 | 7.751773991 | -50 | 50 |
| 5 | 1 | 0 | 7.751773991 | 10.0124922 | -50 | 50 |
上記表では波長0.4μm、マスク面とスクリーン面のギャップ量1000.4μm、照明の広がり角度0.01rad、 X方向min値-10μm、X方向max値10μm、X方向分割数50、Y方向min値-10μm、Y方向max値10μm、Y方向分割数50、 が設定されています。
マスクパターンは５個の矩形パターンが定義されています。U0r[i]はマスク面の波動の実数部です。 通常は1を設定しますが、位相シフトマスクのように位相が180度ずれている場合は-1を設定します。
U0i[i]はマスク面の波動の虚数部です。位相が0度または180度以外の場合、U0i[i]は0以外の値になります。
Xmin[i]、Xmax[i]、Ymin[i]、Ymax[i]は矩形パターンの位置と大きさをμm単位で設定します。
「デフォルト条件」の計算結果
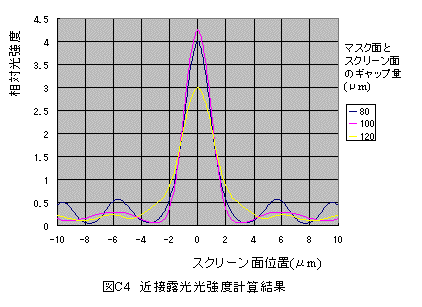
「デフォルト条件」の計算結果を図C4に示します。
図C4から以下のことが分かります。
(1)マスク面とスクリーン面のギャップ量は100μmの場合にスリットの幅は細く、光強度は最大になります。
（2）このスリット光の幅は約3μmであり、約3μmのスリットパターンを形成することができます。
(3)マスク面とスクリーン面のギャップ量が80〜120μmの範囲でスリット光のコントラストは十分得られます。
(4)相対強度は約4であり、集光効果によって光強度は四倍となります。 これは必要な露光時間が1/4となり、スループットが向上することを示しています。
近接露光の応用
近接露光の最大の特徴は、パターンの転写原理が単純で低コストで高スループットの露光装置ができることです。
反面、マスク面とスクリーン面のギャップ量に依存して急激に解像度が劣化します。
従って、大画面の液晶ディスプレイやプラズマディスプレイの製造に適しています。 しかし、高精細の液晶ディスプレイにおいては、より微細なパターンの転写が必要とされています。
「デフォルト条件」のパターン事例は近接露光でもより微細なパターンを転写できる可能性があることをしめしたものです。
しかし、近接露光で「デフォルト条件」で示したテクニックが適用できるパターン形状は限られています。
このようなパターン形状上の制約を軽減する方法としては複数回に分けて露光を行う多重露光方法があります。
近年、後で紹介する投影露光においては位相シフトマスクの使用が一般的になってきています。 位相シフトマスクでもパターン形状上の制約があり、これを回避する手段として多重露光方法が用いられています。
位相シフトマスクの使用に関し、近接露光は投影露光と比較してより厳しい制約が加わります。
トップページに戻る。