多光束干渉エリプソメータは薄膜の膜厚、屈折率、吸収係数の測定に幅広く応用されています。このエリプソメータの測定原理を理解するには、薄膜における多光束干渉を知る必要があります。
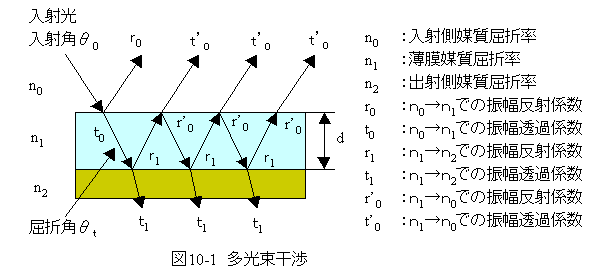
図10-1において、入射光はｎ0→ｎ1面でr0反射し、 t0透過します。ｎ1→ｎ2面ではr1反射し、 t1透過します。 t1は戻ってこないとします。ｎ1→ｎ0面ではr’0反射し、 t’0透過します。この後もｎ1→ｎ2面、ｎ1→ｎ0面の反射と透過が繰り返されます。
従って、トータルの反射（R)は
R=r0 + t0 t’0 r1 + t0 t’0 ( r1 r’0) + t0 t’0 ( r1 r’0)2 +・・ ----(10.1)式
となる訳ですが、光が薄膜を通過する際の位相変化を考慮する必要があります。
薄膜（厚さｄ）を片道通過する際の位相変化をδとすると
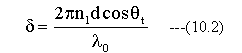
となります。（（10.2）式のcosθｔは一見分母にくるように錯覚します。しかし、 （10.2）式は正しい式です。）
多光束干渉での振幅反射率Rは
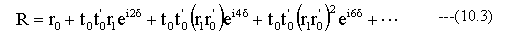
となります。(10.3)式は急速に収束しますのでこのままn次項まで計算すれば実用的な計算精度が得られますが、より計算しやすいように変形することができます。
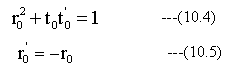
(10.4) (10.5)式の関係式は同一面における入射方向の違いによる振幅反射率と振幅透過率の関係式ですが、 (9.36)～ (9.39)式から導くことができます。
(10.4) (10.5)式を(10.3) 式に代入して整理すると
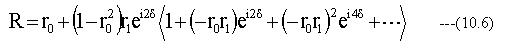
となります。ここで、無限等比級数の関係式(10.7)を用いて(10.6)式を変形します。
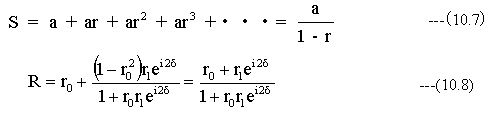
(10.8)式で多光束干渉の振幅反射率を計算できます。反射率強度は
で計算します。なお、振幅反射率ｒ0、ｒ1は(9.36) (9.38)式を用いて計算します。
１１章：エリプソメータに行く。