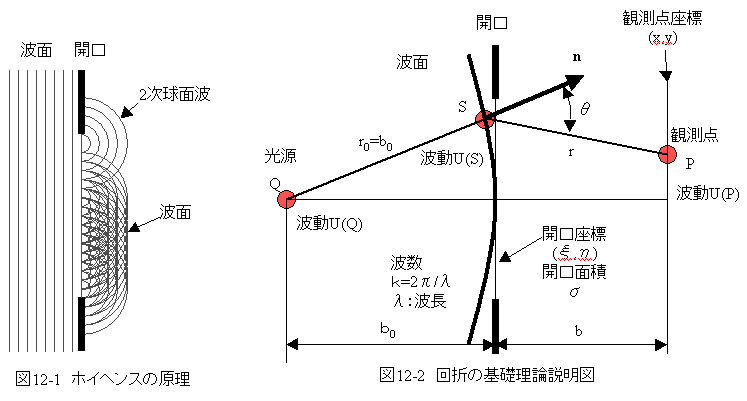
ホイヘンスの回折理論ホイヘンスは回折現象を説明するために、図12-1に示すように「波面上の全ての点から2次球面波が発生し、それらの包絡面が新しい波面を形成する。《とした。これをホイヘンスの原理という。
しかし、 2次球面波は前進する波面と同時に後進する波面が生じるという問題があった。
フレネルはこの問題を解決するために2次球面波の発生方向によって値が変わる傾斜係数K(θ)を導入した。図12-2の回折の基礎理論説明図に示すように開口σ上の位置Sにある微小面積ｄσでの入射光の波動振幅をU(S)で表し、位置Sから観測点Pまでの距離をrとして、2次球面波を次のように表した。
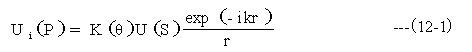
K(θ)が傾斜係数で微小面積ｄσの法線ベクトルｎに対する観測点Pの方向を角度θで表した。 θ＝0のとき値1、θ＝ πのとき値0をもつ傾斜係数を用いることで、後進波の発生を抑制できる。2次球面波は開口のあらゆる点から発生し、その重ね合わせとして回折が記述できる。
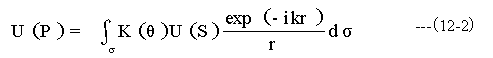
これをホイヘンス-フレネル積分という。
ホイヘンス-フレネル積分は概念的に理解しやすいのですが、U(P)とU（S)の単位が一致しない問題があります。
フレネル-キルヒホッフの回折式フレネル-キルヒホッフの回折式はヘルムホルツの方程式から導き出されます。しかし、誘導の過程は複雑ですので解説は後回しにしたいと思います。
θ0：開口部波面から光源Qに向かう法線ベクトルと線分QSのなす角度
θ1：開口部波面から観測点に向かう法線ベクトルと線分ＳＰのなす角度（法線ベクトルの方向の違いに注意）
その他の記号は図12-2として、回折式は下記の通りとなります。
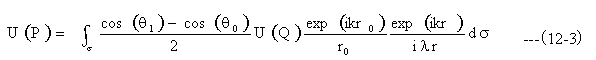
近時的にcos(θ0）≒-1、 cos(θ1）≒1、開口部での波動をU(S)として、(12-3)式を変形して(12-4)式となります。
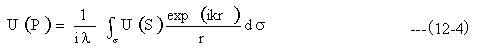
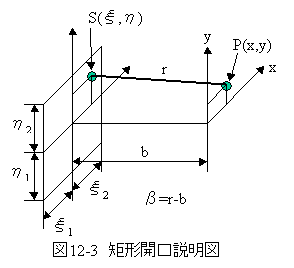
フレネル回折式図12-3 矩形開口説明図で（12-4）式を変形します。
1/r→1/b、
exp(ikr) → exp(ikβ)
とします。
距離bによる位相変化の影響は無視されますが、実用的にはこれで十分な近似精度が得られます。
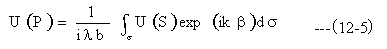
図12-3の矩形開口説明図において
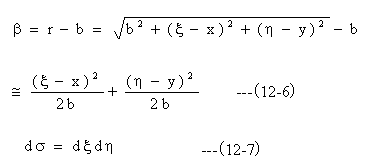
(12-5)式に(12-6)(12-7)式を代入します。
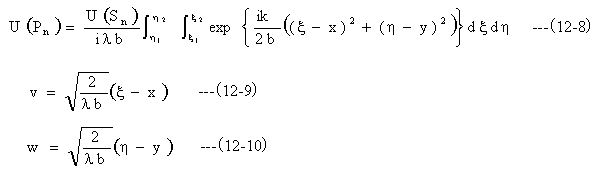
とおいて(12-8)式を変数変換して、整理すると
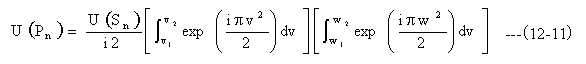
任意のパターン形状のフレネル回折ひとつの矩形開口による観測点Pの波動は(12-11)式に示すように1次元積分の積の形で与えられ大変計算しやすくなります。ここでは、矩形開口内の波動U(Sn)は均一であることが前提となります。
開口を非常に多くの矩形開口の総和として定義することにより、任意のパターン形状、パターンコントラスト、パターンの位相差に対応できます。
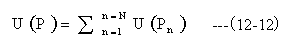
(12-11)(12-12)式により任意のパターン形状の観測点Pの波動を求めます。
光強度観測点Pの光の強度は観測点Pの波動の絶対値の自乗として求めます。
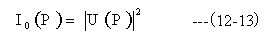
有限の大きさの照明NA（照明角度分布）での光強度（12-13）式におけるI0(P)はパターンに平行光線を垂直に照射した場合の観測点Pの光の強度を与えます。
照明光がパターン面に対して傾いている場合は、観測面における光強度分布がシフトします。従って角度αの照明での観測点Pの光の強度は下記のようになります。
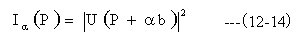
有限の大きさの照明NA（照明角度分布）での観測点Pの光強度は下記のようになります。
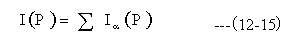
（12-15）式において角度αは照明NAの角度内で均一分布になるように設定する必要がありますが、分割数を大きくしますと計算時間が長くなりますので、サンプル計算プログラムでは１３本で近似します。
スカラー和とベクトル和（12-15）式の加算は波動の加算ではなく、光強度の和になっています。これは異なる光源からでた光線は干渉しないためです。このような加算をスカラー和と呼びます。
逆に同一の光源からでた光は干渉するため波動の総和を求めます。このような加算をベクトル和と呼びます。
フレネル-キルヒホッフの回折式の誘導フレネル-キルヒホッフの回折式の誘導は大変複雑です。（読み飛ばしても問題はありません。）
関数uとｖで表された二つの波に対してヘルムホルツ方程式を記述する。
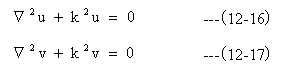
ここで、グリーンの定理を用いる。
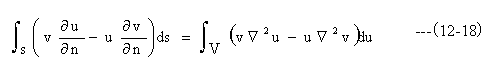
（12-18）式に（12-16）と（12-17）式を代入すると下記の関係式になります。
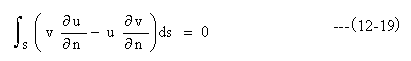
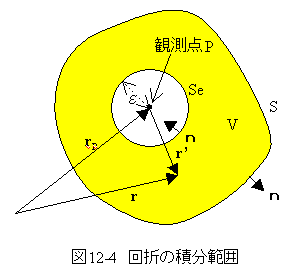図12-4において観測点Pの位置ベクトルをｒｐ
観測点Pを原点とする位置ベクトルをｒ'
関数ｖは観測点Pを点光源とする球面波として
下記式で表す。
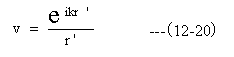
グリーンの定理が成り立つためには、領域V内に特異点を 含んではならない。
このため、図12-4に示すように、点Pを中心とする半径εの 球面Seを考え、この球を積分範囲から取り除くと(12-19)式は 下記のようになる。
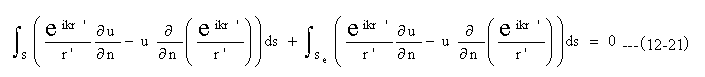
球面Se上では、法線ベクトルｎは球面に垂直で球の内側を向いている。位置ベクトルr’は球面に垂直で外側を 向いている。従って球面Se上では
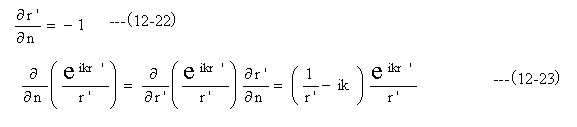
球面Se上ではr’=εであり、極座標に書き換えると
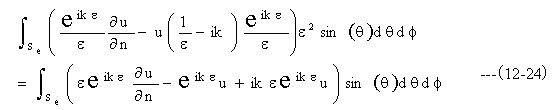
ここでε→0とすると、積分内の第2項のみが残る。またｒ→rpとなる。
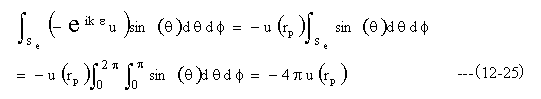
従って（12-21）式よりつぎのキルヒホッフの積分定理が求まる。
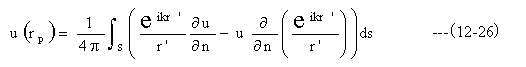
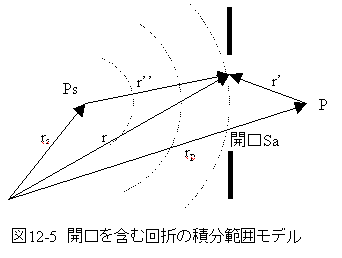
図12-5において、開口Sa面上では、r’>>λ、すなわち k>>1/r’としてよい。
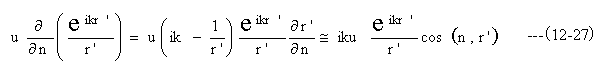
ただし、(n,r’)はnとr’のなす角である。
開口Sa面上の波動uが点Psを点光源とする球面波とすると
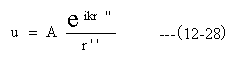
となる。
また、Sa面上では、r’’>>λ、すなわちk>>1/r’’として良い。従って
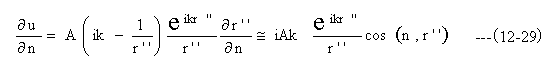
(12-26)式に（12-27）と（12-28）と（12-29）式を代入して整理すると
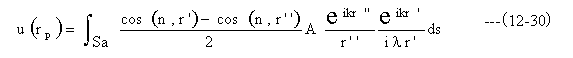
r’とr’’は互いに逆向きである。また法線ｎとなす角は近似的にゼロとしてよい。またSa面での波動関数g(r’’) で置き換えると（12-30）式は以下となる。
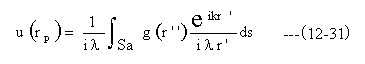
（12-31）式が求める回折の基礎式です。
この式はr’>>λの条件において、成立します。
１３章：近接露光計算演習（１）に行く。