投影光学系における回折理論投影光学系における回折式もフレネル-キルヒホッフの回折式から導くことができます。この場合、理想点光源の投影像が求まります。しかし、複雑なパターン条件、照明NA、レンズ収差を考慮した実用的な計算に適用には適しません。
サンプル計算プログラムでは、フレネル-キルヒホッフの回折式を用いずにフーリエ変換とフーリエ逆変換をもちいます。
光の波動式光は電場と磁場の周期的変化と言われています。
これを式で表わすと、
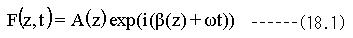
ここでzは距離であり、tは時間です。光の波動は距離(z)と時間(t)の周期関数と表わされ、複素関数と なっています。 波動の絶対値A(z)は球面波の場合、光源からの距離(z)に反比例し、A(z)=A/zの関係があります。
フーリエ変換による計算手法においては、時間項ωtを無視します。
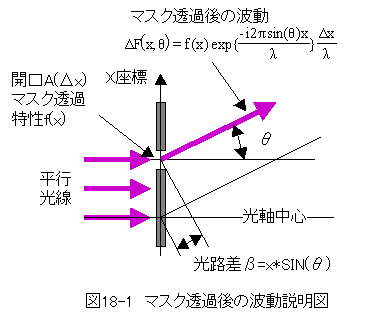
マスク透過後の波動マスク透過後の波動説明図を図18-1に示ます。
図18-1においてマスクに照射する光は平行光線 とし、光強度は１とします。
マスク面上の開口Aの透過特性をf(x)とします。
ここで、f(x)は透過率と位相差を持つ複素関数です。
開口部の無次元化した大きさをΔx/λとします。
座標xを透過した角度θ方向の波動は光軸中心 に対して、光路差β=x*SIN(θ)分の位相遅れが 生じます。
従って、マスク透過後の波動は下記式となります。
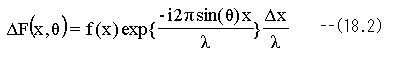
マスクパターンのx1～x2までの領域を通過した光の 波動は(18.2)式の積分で求めることができます。
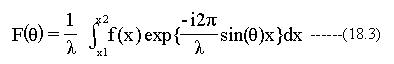
(18.3)式で1次元マスクパターンを通過した光のフーリエ変換像を求めることができます。 (18.3)式は波動であり光強度にする場合は、波動の振幅の絶対値の自乗を求めます。
2次元マスクパターンについては、同様に下記式となります。
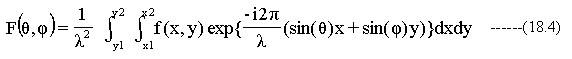
(18.4)式において記号は下記のように定義しています。
λ ：波長
θ ：回折光角度
φ ：回折光角度
f(x,y) ：マスクパターンの光透過特性
x1,x2 ：マスクパターンの範囲
y1,ｙ2 ：マスクパターンの範囲
無収差レンズを通過したベストフォーカスの結像計算式マスクパターンに平行光線を照射するとフーリエ変換面にフーリエ変換像ができます。このフーリエ変換 像はレンズを通過すると焦点位置を球の中心とする球面波に変換されます。
まずは、理想レンズにおける結像を論じたいと思います。
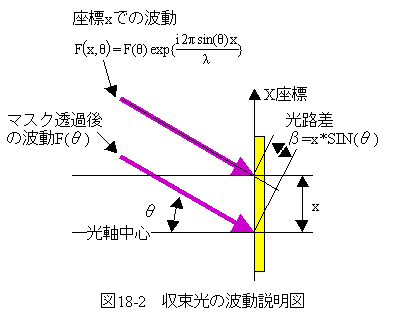
図18-2に理想レンズにおける収束光の波動説明図を示します。
図18-2において光軸中心の波動はフーリエ変換後の 波動と一致します。
無収差、ベストフォーカスの場合、X座標のxの位置では光路差β=x*SIN(θ)を生じます。 （位相が進みEXP(-i)→EXP(i)となります。）
従って、座標xでの波動は下記となります。
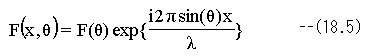
レンズの入射瞳を通過した光の角度範囲をθ1～θ2 とした場合、レンズを通過したx座標の波動は下記と なります。
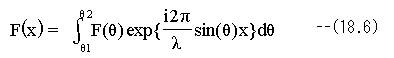
(18.6)式は1次元の式ですが、同様な類推で2次元の式を求めます。
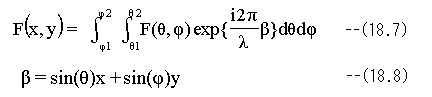
(18.7)(18.8)式が2次元での投影像の波動を与える式です。(18.7)式はほとんどの計算条件で共通ですが、(18.8)式は、計算条件で変化します。(18.8)式は無収差レンズでのベストフォーカスでの投影像の波動を与えます。
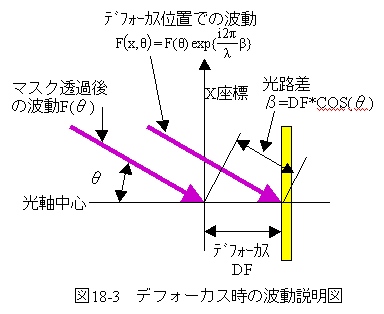
無収差デフォーカスデフォーカスすると光路差βが変化します。この関係説明図を図18-3に示します。
デフォーカスするとベストフォーカス時と比較 して、下記式の光路差が発生します。
また、 cos(θ) は近似的に
が成立します。
光路差において定数1は投影像のコントラストに は影響しません。
光路差がλ/4となるデフォーカス量を求める式は 下記のようになります。
(18.11)式において、θ≒NAとして整理すると 下記のようになります。
(12.12)式は波動光学では有吊な関係式であり、投影光学系の理論焦点深度を与える式です。
すなわち、 (12.12)式は波面の収差量がλ/4となるデフォーカス量を示しています。焦点深度の定義は 見方によってかわりますが、一般的には、波面の収差量λ/4がゆるされる限界とみることができます。
理想点光源の解像度の式波動光学において有吊なもうひとつの式に投影光学系の解像度(R)を与える下記式があります。
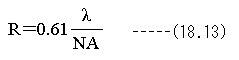
投影光学系での投影像の光強度分布を求める手法としては、フーリエ変換を用いた方法とフレネル-キルヒホッフの回折式を用いた方法があります。
前者は平行光線をマスクパターンに照射することを基本としていますが、後者は理想点光源の投影を基本 としています。
(18.13)式は後者の理想点光源の投影の式展開から誘導できます。(18.13)式の値は理想点光源の投影像の光強度が極小となる半径を示しています。従って、一般のマスクパターンの投影においては定数0.61は厳密な意味を持つ訳ではありません。しかし、解像度の定義は明確にすることが難しいしいため、定数0.61を一般的に用います。
フレネル-キルヒホッフの回折式を用いた投影光学系での投影像の光強度分布計算方法の誘導説明はかなり複雑なものになります。ここでは、 (18.13)式の誘導説明は省略します。
波面収差と光路差β2次元でのデフォーカスを考慮した光路差βの式は下記式となります。
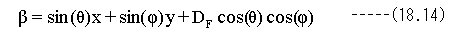
(18.14)式は正確な2次元でのデフォーカスを考慮した光路差βの式です。
(18.14)式の「cos(θ)*cos(φ)《の項は、計算を行う上で少し厄介な形をしています。
この項は2次元での積分計算を1次元に分解できない形です。（計算時間を無視すれば2次元積分は可能。）
ここで、
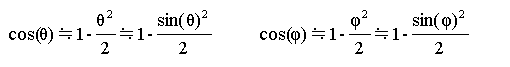
の近似式の関係を用いて、(18.14)式に代入し、定数項と微小項を無視して整理すると
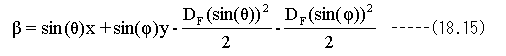
近似式(18.15)式をみると角度変数sin(θ)、 sin(φ)に対して位置変数x,yは1次の関係式になっており、 デフォーカスDFに関しては2次の関係になっています。
言いかえると1次の波面収差は結像位置のオフセットを決定し、2次の波面収差はデフォーカスを決定 します。
光路差βを与える一般式は、
β= β(θ, φ) --------(18.16)
となり、 β(θ, φ) はどのような関数であってもよく、またβ(θ, φ) を実測データに基づく数表でもよいのですがこの場合は、2次元の積分を行う必要があります。
計算で扱いやすい波面収差として、角度変数θ、φの3次関数で与えられる光路差を生じる収差「コマ収差《4次関数で与えられる光路差を生じる収差「球面収差《があります。
「非点収差《「コマ収差《「球面収差《等の１～６次の波面収差の式は下記となります。
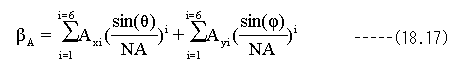
波面収差を考慮した光路差βの式は下記となります。
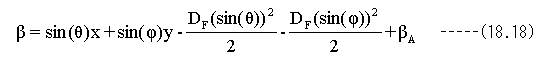
(18.17)式において、NAは投影光学系のNAの最大角度で波面収差を正規化するための定数です。
Ax3はx方向コマ収差で単位はλです。同様にAy3はy方向コマ収差、Ax4はx方向球面収差、Ay4はy方向球面 収差です。
本来は、あらゆる波面収差に応じた投影像の波動（または光強度分布）を求めるべきですが、実際 の計算量を考慮するとある程度の近似式を用いることはやもえません。
(18.18)式はsin(θ)の項とsin(φ)の項が分離しており、1次元の積分に分解可能です。
照明光源の傾斜と広がり以上の説明においては、照明はマスクパターンに垂直に照射する平行光線を前提として、解説しました。
しかし、実際の投影光学系における照明は垂直に照射する平行光線ではなく、照明光源の傾斜と広がりを 持っています。
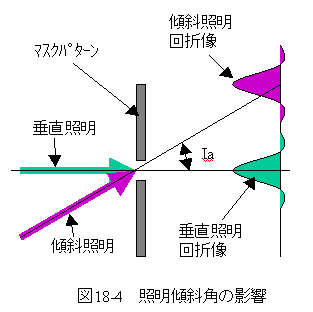
照明の傾斜角の影響関係図を図18-4に示します。
図18-4に示すようにマスクパターンに傾斜した照明 が照射されると回折像の角度は傾斜角度分シフト します。
また、回折像の分布は垂直照明と同じで単純に 中心角度がシフトします。
もう一つ重要な仮定が必要となります。
それは、角度の異なる光が干渉するか？あるいは 干渉しないか？という仮定です。
一般的な条件において、角度の異なる照明は干渉 しないと仮定します。
この仮定は、光源は無限遠（あるいはケーラ照明） にあり、異なる角度の照明は異なる光源からでたと 仮定されます。
異なる光源からの光は時間的に位相がランダムと仮定します。従って、異なる角度の照明は干渉しませ ん。この場合の数学的な処理は、光の波動の和ではなく、光の強度の和として扱います。
俗語かもしてませんが、光の波動の和を「ベクトル和《、光の強度の和を「スカラー和《といって区別 します。
すなわち、干渉性の光を扱う場合は「ベクトル和《の処理を行い、非干渉性の光を扱う場合は「スカラー 和《の処理を施します。
一般に波動光学では、波動の時間項は無視して計算しますが、光の条件によって、 「ベクトル和《と 「スカラー和《の使いわけを行います。
では、照明の傾斜角度が連続的に変化する照明光の広がりがある場合は、どうすればよいでしょうか？
実際には、このようなケースがほとんどです。しかし、投影像の光強度分布を計算するにあたって、 照明角度を連続として計算することはできません。
複数の傾斜角を持つ照明光の「スカラー和《として投影像の光強度分布を計算します。この場合、照明 光線の数を多くすれば誤差が減りますが、計算時間が長くなるためあまり多くもできません。
照明光源の波長分布一般的に照明光源は連続的な波長を持っています。これも上記の角度の異なる照明と同様に「スカラー和《 として扱います。
この場合もより多くの波長について、 「スカラー和《を求めればよいのですが、同様に計算時間が長く なるためあまり多くもできません。
計算式纏め（１）マスクパターンを通過した光のフーリエ変換像の波動
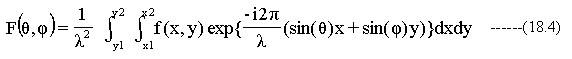
（２）レンズを通過した光の結像の波動
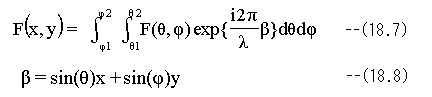
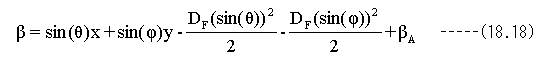
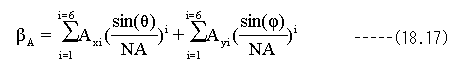
実際の計算式投影光学系の投影像の波動は１２章の(18.4)(18.7)(18.17)(18.16)式で計算できますが、実際の計算プログラムでは計算しやすいように変数変換しています。
フーリエ変換の計算簡略化マスクパターンのフーリエ変換は代数解を求めることができます。代数解による方法は高速で正確です。この条件においては、変数を整数に限定する必要がなく、データエリアの大きさも自由です。
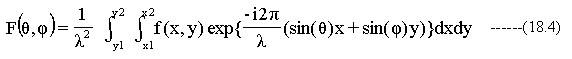
(18.4)式に対しては、下記のように変数変換します。
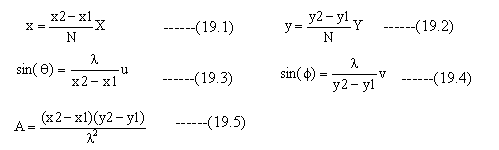
(18.4)式に(19.1)～(19.5)式を代入して、整理すると下記のようになります。
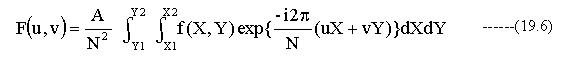
ここで、（ 19.6)式の定数Aは、後で説明する逆変換1/Aの定数と相殺され省略できます。
（ 19.6)式において、f(X,Y)が定数の場合は代数解を求めることができます。矩形パターン内の透過特性が均一の場合はf(X,Y)が定数となります。
f(X,Y)= U0として、 （ 19.6)式の代数解を求めます。
代数解は下記の通りとなります。
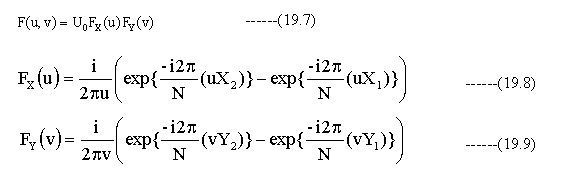
(19.8) (19.9)式を実数部と虚数部に分けて記述すると下記式となります。
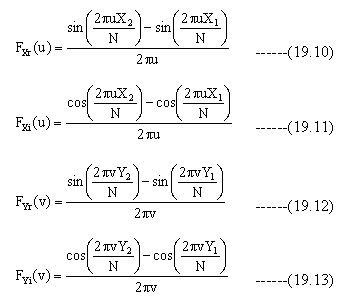
u=0,v=0のときは下記式で計算します。
(フーリエ変換式は、 u=0,v=0のとき指数関数の結果が1となり、簡単に積分できます。）
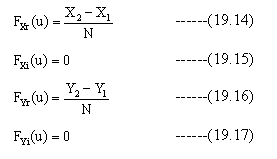
パターンが複数の矩形パターンで構成されている場合
は、 F(u,v)の実数部、虚数部別の総和で求めることができます。
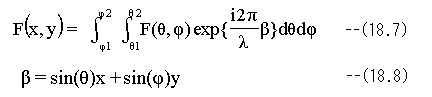
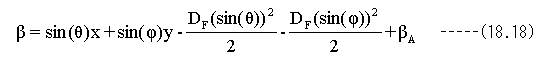
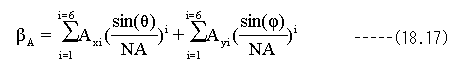
フーリエ逆変換の計算簡略化(18.7)(18.17) (18.16)式に対して、下記のように変数変換します。
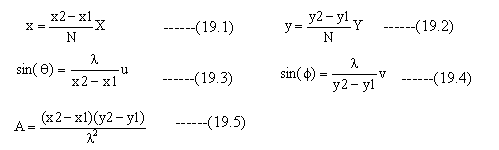
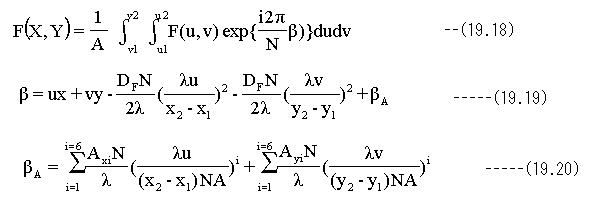
(19.18)式の定数1/Aはフーリエ変換式(19.6)式の定数Aと相殺され省略できます。
(19.18)(19.19)(19.20)式は下記のように1次元の積分形に変形することができます。
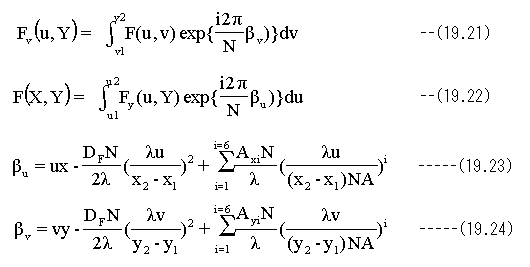
(19.21)(19.22)式は1次元の積分式です。Βuとβvは(19.23)(19.24)式で与えられます。この計算式は複雑なため、代数解を求めることはできません。従って、計算を実行するにあたっては、数値積分法もしくは高速フーリエ変換(FFT)を用いる必要があります。
サンプル計算プログラムではプログラミングが容易な数値積分法を用いて積分を実行しています。数値積分法は計算時間が長くなる欠点がありますが、データ領域を2のN乗にする制限がなく、自由にデータ領域の大きさを設定できる利点があります。
１９章：投影露光演算プログラムに行く。