光線追跡の基礎式幾何光学は以下の三つの前提で成り立っています。
（１）均等な媒質を通過する光は直進する。
（２）個々の光線は互いに無関係で干渉はしない。
（３）異なる媒質の境界を通過する際には、屈折および反射の法則に従う。
屈折の法則は図27-1において
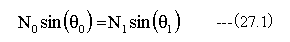
反射の法則は図27-2において
となります。
光線追跡の基本式は（27.1）式と（27.2）式のみです。
あとは、複雑な3次元幾何学で解くことができます。
光路長と波面収差設計した光学系の良し悪しの判断方法として波面収差があります。
波面収差がわかると波動光学の理論から投影像の光強度分布への影響がわかります。
波面収差を求めるためには光路長を計算する必要があります。
図28-3 波面収差説明図において光軸中心の総光路長(Lsｃ)は下記式で計算されます。
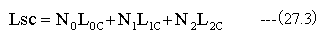
同様に任意の像高さYを通過する総光路長(Lsｙ)は下記式で計算されます。
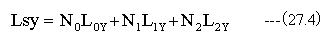
ここで全ての光線が点Pを通過するとすると、光線追跡の結果と矛盾します。なぜなら必ずしも 光線追跡の結果が点Pを通過せずに少しずれた位置を通過するからです。
光線のずれをプロットしたのが「スポットダイアグラム《です。 「スポットダイアグラム《でもおおまかな光学系の評価はできるのですが、波動光学の理論から投影像の光強度分布への影響を求めることができません。
点Pの直前の光線の出射位置と点Pは無理やり直線で結び光路長を計算します。
波面収差（A)は以下の式で計算します。
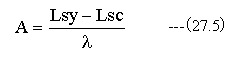
（27.5）式は総光路長の差分を波長（λ）で割っています。従って波面収差（A)の単位は波長（λ）で 表示されます。
（27.5）式の値は像高により複雑に変化しますが、多項式近似を行なって多項式の次数毎の係数 を求めます。
1次の係数がオフセット、2 次の係数がフォーカス、3次の係数がコマ収差、4次の係数が球面収差を 意味します。
２８章 3次元光線追跡計算式の座標系定義に行く。