3次元光線追跡計算式の座標系定義
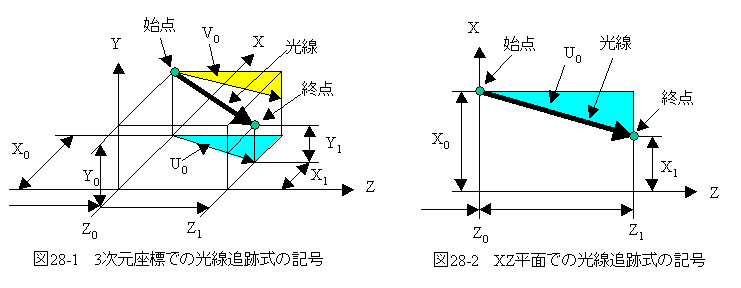
図28-1に3次元座標、図28-2にXZ平面での光線追跡式の記号の関係を示します。
始点（X0,Y0,Z0)から角度(U0,V0)で出た光線は次のレンズ面と交わります。この点を終点（X1,Y1,Z1)とします。 終点では光線は屈折し角度(U1,V1)となって出射します。
次に終点を始点に置き換え、次の終点と終点での角度を求めます。この作業を繰り返すことにより次々と光線の位置と角度を求めることができます。
光線追跡の一般式は下記のようになります。
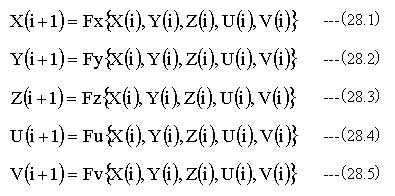
(28.1)～(28.5)式において、関数Fx,Fy,Fz,Fu,Fvの形はレンズの曲率、屈折率、軸間距離等の光学条件によって決定されます。
複雑な図形を図28-1に示すように斜視図で表すのは複雑になって理解しにくいので、図28-2に示すようにXZ平面で表します。
また、図中の記号はX(i+1)=X1、 X(i)=X0として表記します。Y,Z,U,Vにつても同様な表記とします。
２９章：球面レンズの3次元光線追跡計算式に行く。