気体分子運動論気体分子運動論の詳細は下記に詳しく説明されています。
気体分子運動論 - Wikipediaに行く。気体分子運動論から導きだされる重要な公式は
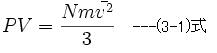
です。（3-1）式において、Pは気体の圧力、Vは気体の体積、Nは総分子数、 mは分子の質量、ｖは分子の平均速度です。
気体定数、アボガドロ定数、ボルツマン定数（１）気体定数
記号 R
意味 気体1molのエネルギーを絶対温度で割った値です。
単位 8.31447 （J ・K-1・ mol-1）
（２）アボガドロ定数
記号 NA
意味 物質量 1 mol とそれを構成する粒子（分子、原子、イオンなど）の個数との対応を示す比例定数
単位 6.02214179(30) × 1023 mol−1
（３）ボルツマン定数
記号 ｋ
意味 分子1個のエネルギーを絶対温度で割った値です。
単位 1.3806504（24） × 10-23 J・K−1
気体定数 R は、ボルツマン定数 k にアボガドロ定数 NA を掛けたものである。
R=ｋ・NA
理想気体の状態方程式気体のモル数をn、Pは気体の圧力、Vは気体の体積、Rは気体定数、Tは絶対温度 とすると、
理想気体は下記の状態方程式を満足する。
P・V＝n・R・T ----（3-2）式
（3-1）式と（3-2）式から
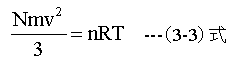
N＝n・NA、k＝R/NAの関係式を用いると（3-3）式 は下記のように変形できる。
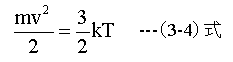
（3-4）式は気体分子1個の運動エネルギーと絶対温度の関係を示しています。
重力場における理想気体の分布温度一定での重力場における理想気体の密度と圧力は下記式で計算できます。
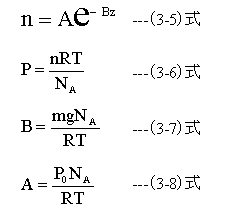
（3-5）式は、分子密度(n)単位（個・m-3を求める式です。
（3-5）式において、AとBは定数、ｚは地上からの高さです。
（3-6）式は、分子密度(n)を圧力（P)単位Paに変換する式です。
（3-6）式において、Rはガス定数、Tは絶対温度、NAはアボガドロ定数です。
（3-7）式は、定数Bを求める式です。
（3-7）式において、mは分子の質量、ｇは重力加速度、NAはアボガドロ定数です。
（3-8）式は、定数Aを求める式です。
（3-8）式において、P0は地上での気圧、NAはアボガドロ定数 、Rはガス定数、Tは絶対温度です。
以下の条件をいれて、具体的な計算をしてみます。
ガス定数 R＝8.31447（J ・K-1・ mol-1）
アボガドロ定数 NA＝6.0221E+23 mol−1
ボルツマン定数 k＝1.38E-23 J・K−1
絶対温度 T＝293.15 °K
N2ガス分子量 mN2=28.0134 ｇ/mol
大気圧 P0=101325 Pa
重力加速度 ｇ＝9.80665 ｍ・ｓ-2
N2ガス分子一個の質量は「m＝mN2/NA《です。
m=4.6517E-26 kg
定数AとBは
A=P0*NA/（RT) ＝2.50347E+25 単位（Pa・J-1)
B=mgNA/(RT) ＝0.00011271 単位（m-1）
上記条件での分子密度(n)と圧力（P)の計算結果を下記表に示します。
| 標高Z(m) | 分子密度(n)個・m-3 | 圧力（P)Pa |
| 0 | 2.50347E+25 | 101,325 |
| 1000 | 2.23663E+25 | 90,525 |
| 2000 | 1.99823E+25 | 80,876 |
| 3000 | 1.78523E+25 | 72,255 |
| 4000 | 1.59495E+25 | 64,553 |
| 5000 | 1.42494E+25 | 57,673 |
| 6000 | 1.27306E+25 | 51,525 |
| 7000 | 1.13736E+25 | 46,033 |
| 8000 | 1.01613E+25 | 41,127 |
| 9000 | 9.0782E+24 | 36,743 |
| 10000 | 8.11055E+24 | 32,826 |
| 11000 | 7.24604E+24 | 29,327 |
| 12000 | 6.47369E+24 | 26,201 |
| 13000 | 5.78366E+24 | 23,409 |
| 14000 | 5.16717E+24 | 20,913 |
| 15000 | 4.6164E+24 | 18,684 |
| 16000 | 4.12434E+24 | 16,693 |
| 17000 | 3.68473E+24 | 14,913 |
| 18000 | 3.29197E+24 | 13,324 |
| 19000 | 2.94108E+24 | 11,904 |
| 20000 | 2.62759E+24 | 10,635 |
| 21000 | 2.34751E+24 | 9,501 |
| 22000 | 2.09729E+24 | 8,489 |
| 23000 | 1.87374E+24 | 7,584 |
| 24000 | 1.67402E+24 | 6,775 |
| 25000 | 1.49558E+24 | 6,053 |
| 26000 | 1.33617E+24 | 5,408 |
| 27000 | 1.19375E+24 | 4,832 |
| 28000 | 1.06651E+24 | 4,317 |
| 29000 | 9.52827E+23 | 3,856 |
| 30000 | 8.51265E+23 | 3,445 |
上記の表から、標高3000mで気圧は地上の約70%、標高6000mで約50% となることがわかります。
人間の生活圏は標高3000m程度までで、標高6000m以上では酸素ボンベ が必要となる訳です。
上記の計算は、理想気体、気温一定、窒素ガスを前提にしていますが、 おおよその実感とほぼ一致します。
（3-5）式は、ポテンシャル場におけるエネルギー粒子の密度を 求める式に変形できます。
（3-5）式において
ポテンシャルエネルギーE（ｚ)＝ｍｇｚ
ボルツマン定数 k=R/NA
の関係式を代入すると
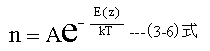
（3-6）式において、nはポテンシャル場におけるエネルギー粒子の密度であり、 Aは任意の定数です。
E(ｚ）は各ｚ位置におけるポテンシャルエネルギー、ｋはボルツマン定数、 Tは絶対温度です。
（3-6）式をボルツマン分布関数と呼びます。
（3-5）式の誘導の過程は省略しました。
（3-5）式の誘導の過程は下記を参照願います。
ボルツマン分布に行く。