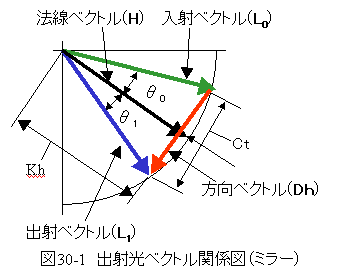
球面ミラーの3次元光線追跡計算式図30-1の球面ミラーの3次元の幾何学条件において、パラメータは下記のとおりです。
入力パラメータ球面レンズと同じです。
光学条件パラメータR1：ミラー面の曲率半径
D0：ミラー面の光軸方向距離
Ox1：ミラーX方向オフセット
Oy1：ミラーY方向オフセット
出力パラメータ球面レンズと同じです。
線と球面の関係式「球面レンズの3次元光線追跡式《と同じになります。
(29.1)～(29.3)式は同じ
ミラー面での反射の関係式(29.1)～ （29.9）式は「球面レンズの3次元光線追跡式《と同じになります。
次に反射の法則から、
が成立します。
図30-1の出射光ベクトル関係図（ミラー）において、入射ベクトルと出射ベクトルの差分ベクトルの絶対値はCtとなります。
方向ベクトル(DH)と法線ベクトル(H)の交点までの距離Khは下記式となります。
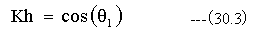
従って、方向ベクトルDｈは下記式となります。
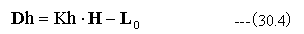
以下の式は「球面レンズの3次元光線追跡式《と同じです。
（ |Dｈ| はDｈの絶対値）
出射ベクトル最終的に求める出射ベクトル(L1)は下記式となります。
ここで、X,Y,Z座標系での出射光線角度U1.V1とは下記の関係式が成立します。
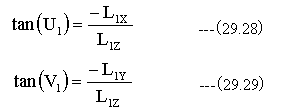
以上の式により、出射ベクトル(L1)を求めることができます。
上記式の一部は一般的になじみの薄いベクトルの式で表わしており、実際の計算は、XYZ成分に 分けて計算する必要があります。また、ベクトルは方向を持っており、数値の正負の方向に十分注意が 必要です。
実際の計算式実際の計算式はベクトルの式を展開して計算する必要があります。
実際の計算式はＣ言語で記載しています。
下記（光線追跡ﾒｲﾝｿｰｽ.txt）をクリックして、サブル＊チン（標準レンズ）を参照してください。
光線追跡ﾒｲﾝｿｰｽ.txt
を参照願います。
３１章：透過傾斜平面板の3次元光線追跡計算式に行く。