光エネルギーの謎光エネルギーについては下記に簡単に記載されています。
光エネルギー - Wikipediaに行く。説明の内容は以下の通りです。
光エネルギー（ひかりエネルギー、light energy）とは、電磁波の一種である光がもつエネルギーを指す。単位はジュール(J)。光エネルギーは光に含まれる光子の数と光子の周波数（波長）によって決まる。
光子のエネルギーはその振動数によって決まり、以下のように表される。
E=h・ν=h・c /λ
h : プランク定数
E : エネルギー
ν : 振動数
c : 光の速さ
λ : 波長
上記の計算式は、多くの実験で有効性が確認されています。
しかし、なぜこの計算式が成立するのか？説明が上十分です。
光が電磁波であるとした場合、波動光学では光のエネルギーを 波動（電場の振動）の自乗として求めるのが一般的です。
厳密には電場ベクトルと磁場ベクトルの外積とすべきですが、 結果的には、一致するようです。
光が電磁波であるとした場合の光エネルギーの詳細検討は下記で 詳しく説明されています。
電磁気学に行く。水素原子の発光スペクトル光子は原子や分子で起こる現象をよく説明できますが、空間での伝播の説明には 向きません。
逆に波動は空間での伝播を良く説明できますが、原子や分子で起こる現象をよく説明できません。
何とかして、光子と波動が融合できるモデルを考える必要があります。
電磁気学はモデルが明確ですが、光子のモデルは極めて曖昧です。
曖昧なモデルは理解しがたいのです。光子の計算結果がいくら正確であっても 騙されていないか？
というふあんが残ってしまいます。
まずは、水素原子の発光スペクトルについて検討してみましょう！！
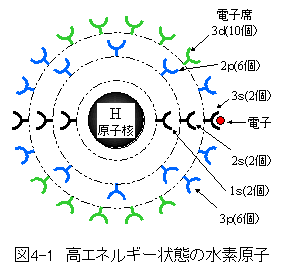図4-1に高エネルギー状態の水素原子モデルを示します。図4-1において、水素原子核のまわりには電子が収まる電子席が配置されています。
（１）第1列には1ｓの電子席が2個あります。
（２）第2列には2ｓの電子席が2個、2pの電子席が6個あります。
（3）第3列には3ｓの電子席が2個、3pの電子席が6個、3dの電子席が10個あります。
（４）ｓ、p、d、ｆはそれぞれ異なる「運動エネルギー《を持ちます。
（５）電子席の「総エネルギー《は「ポテンシャルエネルギー《+「運動エネルギー《となります。 （６）電子席の「総エネルギー《の低い順は1s→2s→2p→3s→3p→4s→3d→4p→5s→4d→5p→6s→4f→となります。
（７）電子は電子席の「総エネルギー《の低い順に埋まっていきます。
図4-1においては、電子が電子席3sに収まっています。
この状態は上安定であり、より「総エネルギー《が小さい電子席が空いている場合は 「総エネルギー《が小さい電子席に移動しようとします。
もし、電子がより「総エネルギー《が小さい2ｓに移動したらどうなるでしょう？。
2ｓのポテンシャルエネルギーは3ｓより小さいため、エネルギーがあまってしまいます。
あまったエネルギーは電子の運動エネルギーに変換されるはずです。
しかし、2ｓが許容する運動エネルギーは零です。
電子席が許容しない電子の運動エネルギーは電磁波として放出されるはずです。
しかし、なぜ？放出されるエネルギーが光の周波数に比例するのでしょうか？
図4-1のような単純な電子席構造では、うまく説明できません。
電子席構造に一定の制限を加える必要があります。
電子席で運動する電子の軌道は決まっており、決められた軌道上を運動できると する必要があります。
この場合、移動した電子席のエネルギー差が大きいほど、電子の運動速度は大きく なり、周波数が大きくなることになります。
図4-2に電子席軌道概念図を示します。図4-2において、電子は軌道上を円周運動をすることができます。
電子が円周運動をすると水平方向からみた場合、電子がが単振動して いるようにみえます。
電子が単振動すると電場と磁場の振動が発生します。 電場と磁場の振動は電磁波となります。 （シンクロトロン放射の原理と同じです。）
以下は、
原子スペクトルの観察と波長の測定に行く。の抜粋です。
電子席ｓ1とｓ2のエネルギー差は大きく、電子席ｓ1での発光は紫外線となります。 これをラインマン系列といいます。
電子席ｓ3からｓ2の電子移動では赤の発光が見られます。これをバルマー系列 といいます。
水素原子は，可視領域に図１のような線スペクトルがあり，バルマー系列と呼ばれている。 波長の長い方からＨα，Ｈβ，Ｈγ，…と吊づけられ，それらの波長λは簡単な一つの式
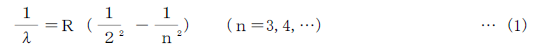
で表わされる。ここで，Ｒはリュードベリ定数と呼ばれる定数（(3)式）である。Ｈα，Ｈβ， Ｈγ の各波長は，この式でｎ＝３，４，５と置いたものになっている。
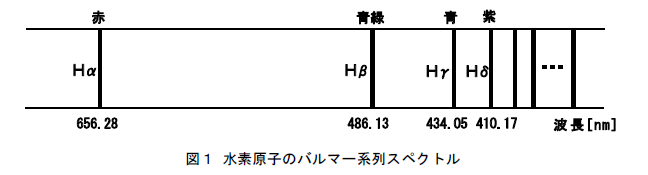
水素原子の発光スペクトルの式(1)は，ボーアの原子モデルによって説明することができる。 このモデルでは，水素原子のエネルギー準位は
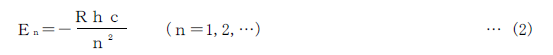
となる。Ｒはリュードベリ定数であり，
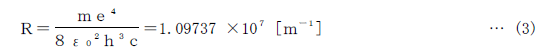
である。ここで，ｍとｅは電子の質量と電荷，ｈはプランク定数，ｃは光速，ε０は真空の誘 電率である。放電によって高いエネルギー準位Ｅｎに励起されれた電子が，より低いエネル＊ 準位Ｅｍに遷移するとき，そのエネルギー差
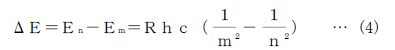
の光子を出す。この光子の振動数をνとすると，エネルギーは ｈνであるから，ν＝ΔＥ/ｈ。また，波長λは，λ＝ｃ/ν＝ ｈｃ/ ΔＥ となる。従って，
と表せる。ここで，ｍ＝1，2，…，ｎ＝ｍ＋1，ｍ＋2，… である。バルマー系列のスペク トルについては，電子はｍ＝２の定常状態に遷移し，このとき，(5)式は先の(1)式となる。 リュードベリ定数を(1)式を用いて波長の実験値から求め，それが理論値(3)に一致すれば， ボーアの原子モデルの正当性が確かめられたことになる。
以上の説明は、電子席から電子席への電子を移動を前提に説明しています。 この場合、発光スペクトルはとびとびの波長となります。
しかし、電子が電子席から飛び出さずに電子席内で運動エネルギーを 持った場合、エネルギーは連続的に変化します。
この場合の発光スペクトルは連続的となります。
光エネルギーまとめ（１）光エネルギーは周波数に比例する。
（２）原子からの発光スペクトルはびとびの波長となることがある。
（３）原子からの発光スペクトルは連続変化ともなりうる。
（４）光エネルギーは電磁波として放出される。
（飛び出すのは光子（粒子）では無い。）
発光、吸収は量子的ですが、エネルギーの伝播は電磁波となります！！
これが光子と波動が融合モデルの考え方です。