黒体輻射の式図5-1ににプランクが提唱した黒体放射の式を示します。
図5-1の式は単位時間（ｓ）・単位面積あたり放出エネルギーを波長幅Δλで割ったものです。（波長幅を掛けると単位時間（ｓ）・単位面積あたり放出エネルギーとなります。）
図5-2に放出エネルギーの計算結果を示します。
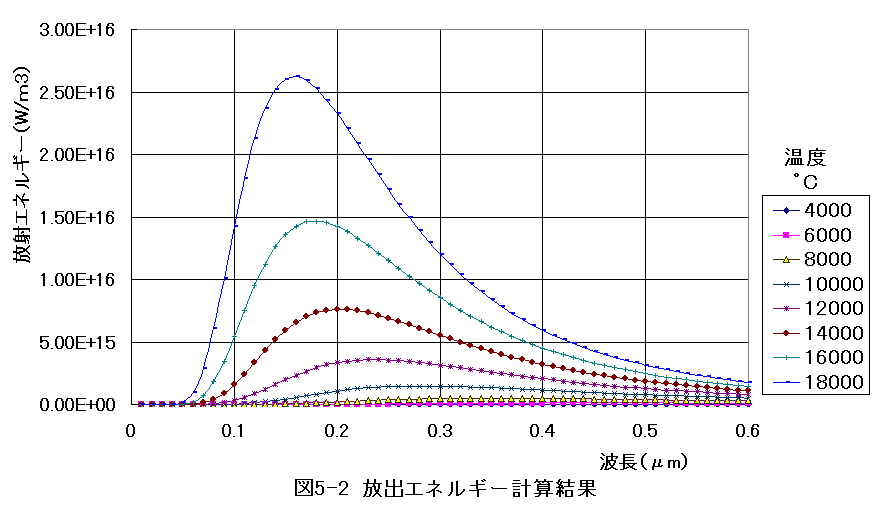図5-2において、表面温度4000℃でのピーク波長は600nmで赤色です。
表面温度6000℃でのピーク波長は470nmで紫色です。
表面温度8000℃でのピーク波長は350nmの紫外線です。
表面温度10000℃でのピーク波長は280nmの紫外線です。
表面温度12000℃でのピーク波長は240nmの紫外線です。
表面温度14000℃でのピーク波長は200nmの紫外線です。
表面温度16000℃でのピーク波長は180nmの紫外線です。
表面温度18000℃でのピーク波長は160nmの紫外線です。
図5-2は高温での発光スペクトルですが、低温の場合 遠赤外線が放出されます。
波長と光のエネルギーの関係図5-3に波長と光のエネルギーの関係を示します。
光のエネルギー（E)は下記式で定義されます。
E=hν＝ｈｃ/λ
ｈはプランク定数、νは光の振動数、ｃは光速、λは光の波長です。
光のエネルギーの単位はeVで示しました。
黒体輻射の式の誘導黒体輻射の式がいかにして誘導されたか検討してみましょう。
まず、光のエネルギーは「E=hν《の整数倊とします。
iを1～∞の整数として、光のエネルギーは
E=ihν ---（5-1）式
となります。
「E=ihν《のエネルギー粒子の 密度分布はボルツマン分布関数で求めることが出来ます。
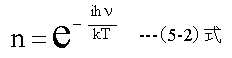
（5-2）式のiは1～∞の整数です。
iが1～∞でのエネルギー平均値は下記式でもとめることができます。
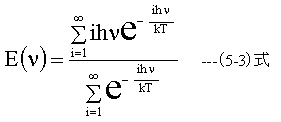
（5-3）式はエネルギー「E=ihν《の加重平均の式になっています。
（5-3）式を下記の多項式の積の公式を使って変形します。
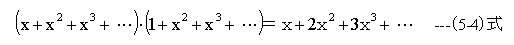
（5-3）式を（5-4）式で変形すると
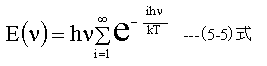
さらに無限等比級数の公式を使って変形します。
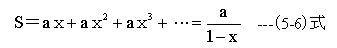
（5-5）式を（5-6）式で変形すると
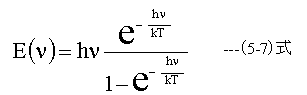
となる。
つぎに、振動数がν+dνの間の単位体積あたりの波の数 ｇ（ν）dνは
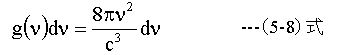
（5-8）式を考慮し、単位体積あたりのエネルギーは
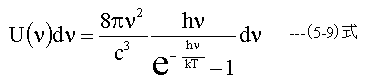
となる。
周波数νを波長λに変換すると
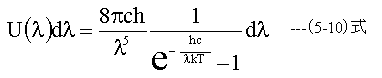
となる。
単位体積あたりのエネルギーと単位面積あたりの放出エネルギーの 関係は
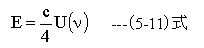
であり、これから
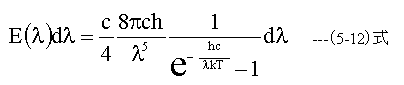
となる。
以上の式の展開はみごとであり、実験値とよく一致する式として しられている。
式の誘導の前提として、光のエネルギーをhνの整数倊と しており、量子論の基礎となっている。
光のエネルギーをhνの整数倊としているが、論じているのは 放出エネルギーと光の周波数の関係である。
どのような形態で光が放出されるかは論じていない。
光が波なのか粒子なのかは、黒体放射の式からはふ明である。
なぜ？高温物体は光を放出するのか？黒体放射の式は高温物体からどのような発光スペクトルが得られるかを 教えてくれます。
しかし、なぜ？高温物体は光を放出するのか？の疑問にたいしては 答えてくれません。
図5-4にヘリウム原子の衝突のモデルを示します。
原子どうしが衝突すると原子全体の運動エネルギーが 電子の運動エネルギーに変換されるとします。
反対方向の正面衝突の場合、原子全体の速度が それぞれ零になります。
エネルギー保存の法則が成立するためには、電子の運動エネルギーに変換 される必要があります。
電子の運動は電磁波を発生しエネルギーを放出します。
ここで、放出される光のエネルギーはhνの関係を満足する 必要があるのですが、電子席は特別の仕組みをもっていて、 hνの関係を満足するように電子の運動エネルギーを 与えているとおもわれます。
６章：光の質量・運動量の上思議に行く。