ローレンツの理論ローレンツは物質の屈折率変化は、光の電場によって原子または分子の 電気双極子が発生するとした。
マクスウェルの方程式において、電磁波が伝播する物質の特性は下記の 物質方程式で記述されます。
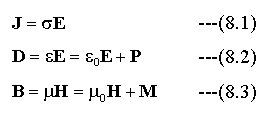
ここに、電場E、磁場H、電気変位D、磁気誘導B、電流密度J、 ρは電荷密度、σは導電率、εは物質の誘電率、ε0は真空の誘電率で8.854×10-12F・m-1、μは物質の透磁率、μ0は真空の透磁率で1.257 ×10-12H・m-1です。また、Pは原子・分子の電荷分布が変化して生じる分極、Mは磁化分布が変化して生じる磁化です。
また、誘電体の屈折率は
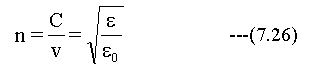
の関係式があります。（Cは真空中の速度、ｖは物質中の速度）
（8.1）式と（7.26）式から下記の関係式が得られます。
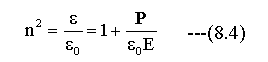
次に原子または分子の運動方程式を考えます。
電子の質量をm、バネ定数をs、粘性抵抗をb、電子の電荷をq、電場をEとします。
この時の運動方程式は
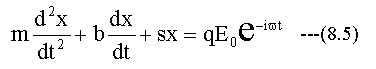
変形して
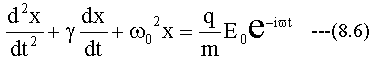
となります。
（8.6）式の微分方程式を解くには、下記の(8.7)式を（8.6）式に代入します。
定数AとBを求め整理すると
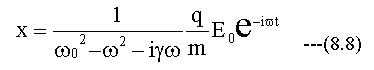
従って、分極Pは
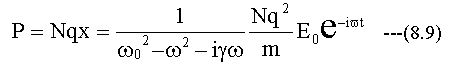
となります。
(8.4)式と（8.9）式から
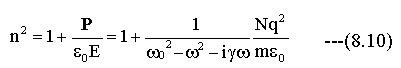
変形して
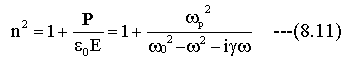
（8-11）式によれば、任意の角速度ωにおける複素屈折率nは、3個の定数で 決定できることになります。
ω0は固有振動角速度、ωpはプラズマ振動角速度、 γは粘性係数です。
これは、物質に依存する定数です。
実測値と計算値の比較材料はシリコンとしました。
とりあえず
λ0=300nm
λｐ=90nm
γ=5.00E+13
として計算してみました。
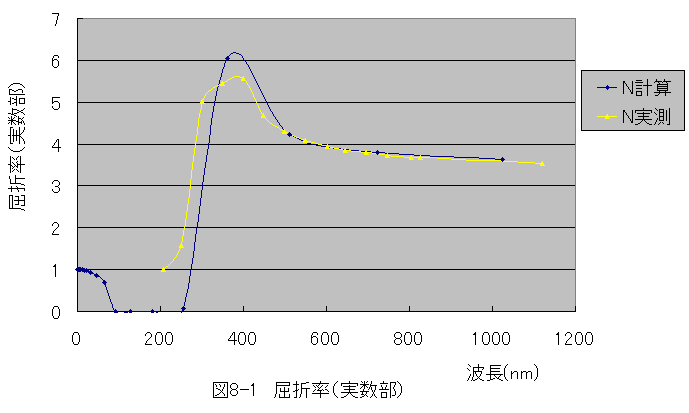
下記表においてNは屈折率の実数部
KはNは屈折率の虚数部です。
| 波長nm | N計算値 | N実測値 | K計算値 | K実測値 |
| 206.6 | 0.02 | 1.01 | 3.004 | 2.909 |
| 250 | 0.06 | 1.58 | 4.924 | 3.632 |
| 300.9 | 29.94 | 5.02 | 14.926 | 3.979 |
| 350.2 | 6.54 | 5.442 | 0.082 | 2.989 |
| 400 | 5.14 | 5.57 | 0.034 | 0.387 |
| 449.2 | 4.59 | 4.682 | 0.021 | 0.149 |
| 499.9 | 4.29 | 4.298 | 0.015 | 0.073 |
| 548.6 | 4.10 | 4.089 | 0.012 | 0.044 |
| 601.9 | 3.97 | 3.943 | 0.010 | 0.025 |
| 645.8 | 3.89 | 3.858 | 0.009 | 0.017 |
| 696.5 | 3.83 | 3.787 | 0.008 | 0.013 |
| 746.9 | 3.77 | 3.736 | 0.007 | 0.009 |
| 805.1 | 3.73 | 3.688 | 0.006 | 0.006 |
| 826.6 | 3.71 | 3.673 | 0.006 | 0.005 |
| 1120 | 3.60 | 3.536 | 0.004 | 0 |
X線領域の屈折率λ0=300nm
λｐ=90nm
γ=5.00E+13
としてX線領域の屈折率（実数部）を図8-1に示します。
屈折率（虚数部）を図8-2に示します。
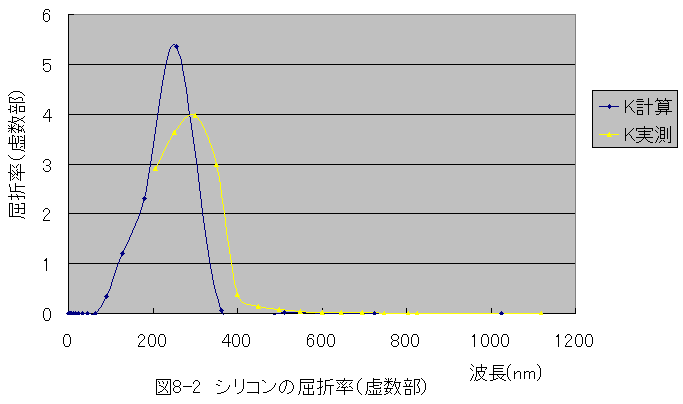
図8-1と図8-2から、X線領域では、屈折率（実数部）は1、 屈折率（虚数部）は0となることがわかります。
光は、波長50nm～380nmの間で強く吸収され、赤外線、X線領域 では透過しやすいことがわかります。
９章：反射と屈折の法則に行く。