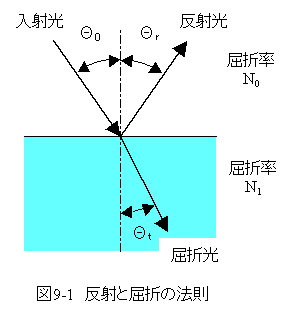
光の反射と屈折は日常的に観察される現象です。
まずは、反射と屈折の法則についてまとめてみましょう。
図9-1において、反射光の角度Θrは
Θr=Θ0 ----(9.1)式
の関係があります。
また、屈折光の角度Θtは
Nt・sin(Θt)=N0・sin(Θ0) ----(9.2)式
の関係があります。
では、反射光と屈折光の光強度はどうなるでしょうか?
垂直入射時の反射率Irは下記式で計算できます。
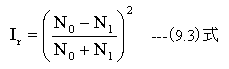
斜め入射の場合に反射率はどうなるでしょう?
斜め入射の場合はS偏光(電場の振動方向が水平面と平行)とP偏光(電場の振動方向が水平面と直角) で反射率が異なります。
P偏光反射率(Irp)、S偏光反射率(Irs)は下記式で計算できます。
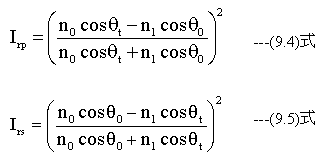
透過率は
透過率=1-反射率 ----(9.5')式
となります。
石英ガラスの屈折率は波長632.8nm(He-Ne)において
屈折率(実数部)N=1.457059
屈折率(虚数部)K≒0
です。
計算結果を図9-2に示します。
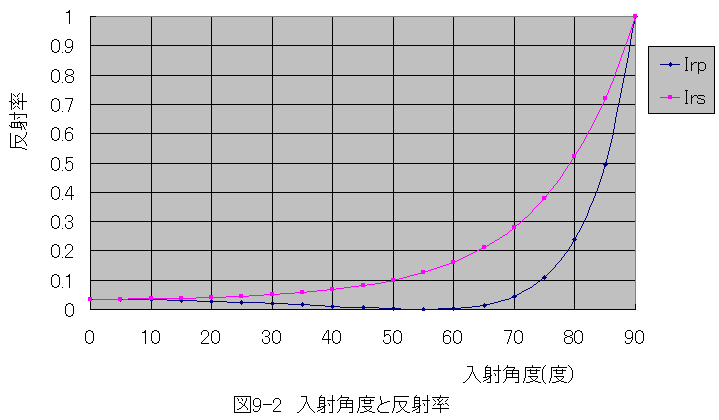
図9-2において、S偏光は入射角度が大きくなるに従い反射率が単調増加します。
P偏光は入射角度が60度付近で反射率が最小となり、その後急に増加します。
反射の式の誘導はマクスウェルの方程式から展開する必要があり、 大変やっかいです。
実用的には読みとばしても問題ありません。
(1)波数ベクトル(K)と電界ベクトル(E)と磁界ベクトル(H)
反射と屈折の関係は電磁波の反射、屈折面の境界条件から、導かれます。電界ベクトル(E)と磁界ベクトル(H)は反射、屈折面に対して任意の角度θ0で入射するとします
。 この関係図は3次元となりますので下記のように製図図法で表します。
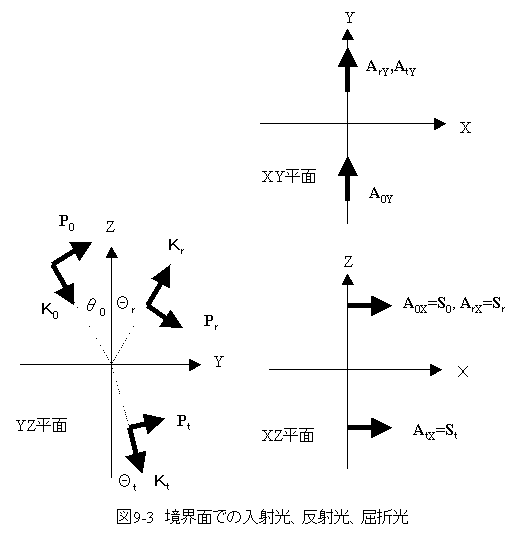
図9-3の境界面での入射光、反射光、屈折光においてK0,Kr、Ktは、それぞれ入射光、反射光、屈折光の波数ベクトルを示します。
入射角、反射角、屈折角をそれぞれθ0 、 θr 、 θtとします。YZ平面に平行な電磁波の電界ベクトルをそれぞれP0 、 Pr 、 Ptとします。またYZ平面に垂直な電磁波の電界ベクトルをそれぞれS0 、 Sr 、 Stとします。
任意の位置ベクトルをr=(X,Y,Z)とします。
図9-3において、入射光、反射光、屈折光の電界ベクトル定数は下記の関係となります。
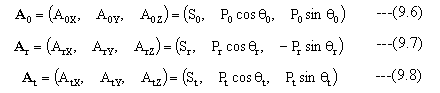
入射光、反射光、屈折光電磁波の波数ベクトル定数はそれぞれ、下記となります。
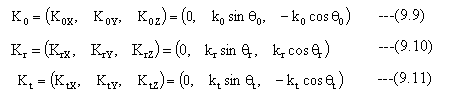
入射光、反射光、屈折光電磁波の電界はそれぞれ、下記となります。
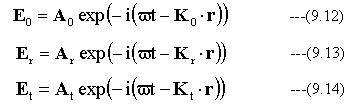
(2) 反射角と屈折角の条件式
(9.12)(9.13)(9.14)式が境界面上(Z=0)の任意の位置Yで成り立つためには
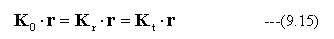
が成り立たなければならない。入射光と反射光の関係において、媒質が同じでありk0=krとなる。また Z=0の関係を用いると
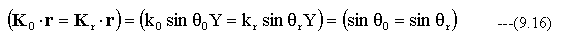
(17.11)式は入射角と反射角が等しいことを示しており、反射の法則である。入射光と屈折光の関係において
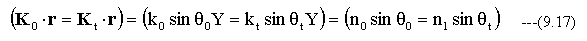
(9.17)式のn0、n1は屈折率であり、入射角と屈折角の関係を示している。この関係は屈折の法則あるいはスネルの法則と呼ばれる。
(3) 境界面における電界ベクトルの条件式
境界面上(Z=0)において、両側の境界面近傍の電界ベクトルは等しくなければならない。従って

(9.18)式のX成分は
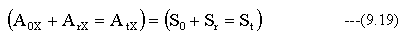
(9.18)式のY成分は
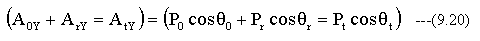
(4) 境界面における磁界ベクトルの条件式
境界面上(Z=0)において、両側の境界面近傍の磁界ベクトルは等しくなければならない。従って

関係式(μ0ωH=K×E)を用いて(9.21)式を書き直すと
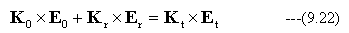
K0×E0は
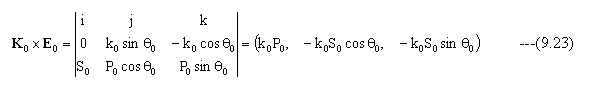
Kr×Erは
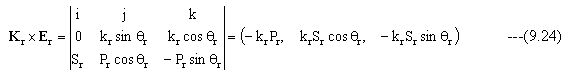
Kt×Etは
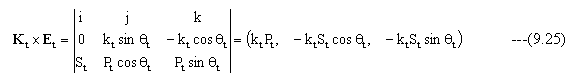
入射と反射の媒質は同じであることから、kr=k0、θr=θ0となる。X方向成分から下記の条件式が成立する。

同様にY方向成分から下記の条件式が成立する。
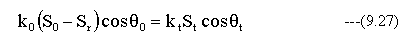
条件式 (9.19) (9.20) (9.26) (9.27)を整理すると
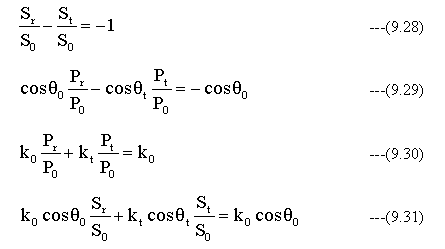
(9.29)(9.30)式から
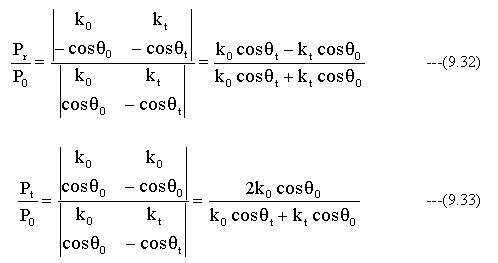
(9.28)(9.31)式から
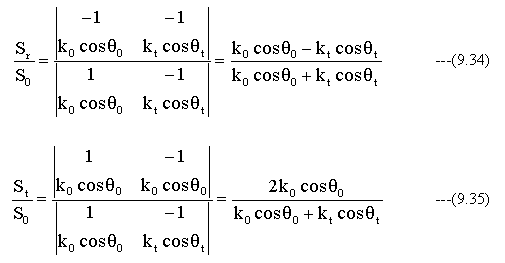
(9.32) (9.33) (9.34) (9.35)式でP偏光の反射光の波動(Pr/P0)、屈折光の波動(Pt/P0)およびS偏光の反射光の波動(Sr/S0)、屈折光の波動(St/S0)を求めることができる。
また、入射光の波数k0、屈折光の波数ktはそれぞれ入射側の媒体の複素屈折率n0、屈折側の複素屈折率n1に置き換えることができる。
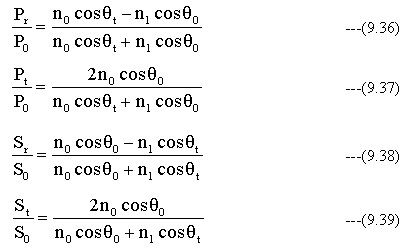
入射光が垂直の場合はθ0= θt=0となり、P偏光とS偏光の区別はなくなる。

n0>n1の場合、反射光波動の符号が負になるが、これは図9-3 で定義した反射光波動のベクトルの方向と逆になることを示している。(反射で180度位相が反転することを示します。)
反射率は波動の絶対値の自乗で計算します。
しかし、透過率は波動の絶対値の自乗とはなりません。
なぜでしょうか?
光強度Iは、誘電率をε、電場をEとして
I= ε・E2 ----(9.42)
となり、反射の場合は誘電率をεが同じですので誘電率εの影響が無視できますが、透過の場合は 誘電率ε変化を考慮する必要があります。
透過率=1-反射率 ----(9.43)
で計算するのが賢明です。
反射率の式の誘導は思ったより大変でした。これは、マックスウェルの方程式が3次元ベクトルの式で難解であり、行列式まで使用したためです。