連立方程式の消去法まずは連立数４（4元）の連立方程式の例で説明します。
A11X1+ A12X2 + A13X3 + A14X4 = B1 -----(1.1)
A21X1+ A22X2 + A23X3 + A24X4 = B2 -----(1.2)
A31X1+ A32X2 + A33X3 + A34X4 = B3 -----(1.3)
A41X1+ A42X2 + A43X3 + A44X4 = B4 -----(1.4)
(1.2) (1.3) (1.4)式の両辺にA11をかけると
（ A21X1+ A22X2 + A23X3 + A24X4 ） A11= B2 A11 -----(2.2)
（ A31X1+ A32X2 + A33X3 + A34X4） A11 = B3 A11-----(2.3)
（ A41X1+ A42X2 + A43X3 + A44X4 ） A11 = B4 A11-----(2.4)
(1.1)式を変形すると
A11X1＝- A12X2 - A13X3 - A14X4 + B1 -----(2.1)
(2.2) (2.3) (2.4)式に(2.1)式を代入して整理すると
（A22 A11 - A12A21） X2 +（A23 A11 - A13A21 ） X3 +（ A24 A11 - A14A21 ）X4 = B2 A11 - B1A21 -----(3.2)
（A32 A11 - A12A31） X2 +（A33 A11 - A13A31 ） X3 +（ A34 A11 - A14A31 ）X4 = B3 A11 - B1A31 -----(3.3)
（A42 A11 - A12A41） X2 +（A43 A11 - A13A41 ） X3 +（ A44 A11 - A14A41 ） X4= B4 A11 - B1A41 -----(3.4)
A22= A22 A11 - A12A21、 A23 ＝ A23 A11 - A13A21 、 A24 ＝ A24 A11 - A14A21 、 B2 ＝ B2 A11 - B1A21 、--------として(3.2) (3.3) (3.4)式を置き換えると
A11X1+ A12X2 + A13X3 + A14X4 = B1 -----(4.1)
A22X2 + A23X3 + A24X4 = B2 -----(4.2)
A32X2 + A33X3 + A34X4 = B3 -----(4.3)
A42X2 + A43X3 + A44X4 = B4 -----(4.4)
同様な操作を繰り返すと
A11X1+ A12X2 + A13X3 + A14X4 = B1 -----(5.1)
A22X2 + A23X3 + A24X4 = B2 -----(5.2)
A33X3 + A34X4 = B3 -----(5.3)
A44X4 = B4 -----(5.4)
の形式に変形できます。
以上の操作を一般化します。
ここで、iとjを1〜nの整数として、
Aij、Bi、Xjとする。
また、消去操作の回数をkとし、1〜n-1の整数とする。
一般化した変換式は下記となる。
Aij=AijAkk-AkjAik ---（6.1）
Bi=Bi Akk-BkAik ---（6.2）
（6.1） （6.2）式において、iはk+1〜nの間で変化する。jは1〜nの間としても実害がない。
連立方程式の後退代入(5.1) (5.2) (5.3) (5.4)式から、X1、X2、X3、X4は容易に求めることができます。
X4 = B4 /A44 ----（7.1）
X3 = （B3 - A34X4 ） /A33 ----（7.2）
X2 = （ B2 - A23X3 - A24X4 ） /A22 ----（7.3）
X1= （ B1 - A12X2 -A13X3 - A14X4 ） /A11 ----（7.4）
（7.1） （7.2） （7.3） （7.4）式を一般化すると下記のようになります。
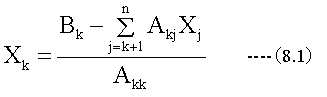
(8.1)式において、ｊはk+1〜nの範囲で変化します。
２章：C言語とVBAの比較に行く。