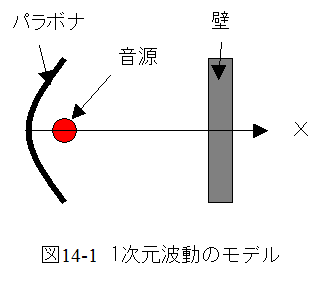
1次元波動のモデル図14-1に1次元波動のモデルを示します。図14-1は超音波レベル計の原理であり。音源からでた音波はパラボナで反射して平面波となって進行し、壁で反射して戻ってきます。
音波の発射時刻と反射波の受信時刻の差から壁までの距離を計測します。
音波の振動数は30kHz程度であり、20℃における空気の音速は約343mです。従って音波の波長は約11mm程度となります。
実用的には波動方程式を解く必要はないのですが、このモデルでの波動方程式の解を検討してみたいと思います。
境界条件は
X=0、ｔ=<t1でφ=sin(ωt)、t>ｔ1でφ=0
x=L、全てのｔにおいてφ=0
となります。
1次元波動導方程式1次元波動導方程式は
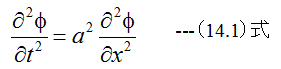
で与えられます。（14.1）式において、φが圧力、ｔが時間、xが音源からの距離です。aは音速で343m/sとなります。
1次元波動方程式の計算方法今任意の関数φ(x,ｔ)を考え、微小量Δxだけ位置を変化させた場合
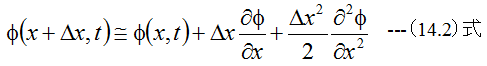
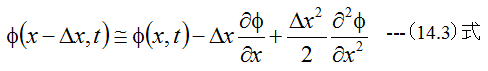
が成立します。（14.2）と（14.3）式を加算すると
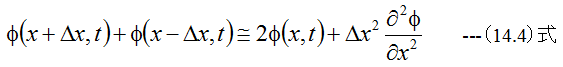
となります。また関数φ(x,ｔ)を考え、微小量Δｔだけ位置を変化させた場合
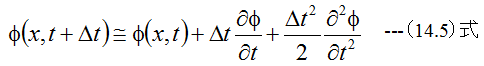
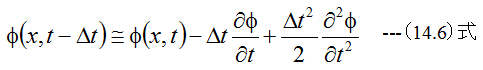
が成立します。（14.5）と（14.6）式を加算すると
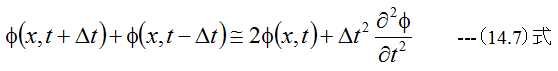
の関係式が得られます。（14.1）式に（14.4）式と（14.7）式を代入して整理すると
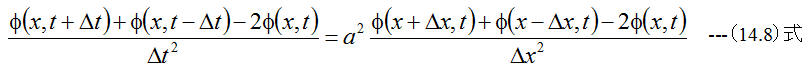
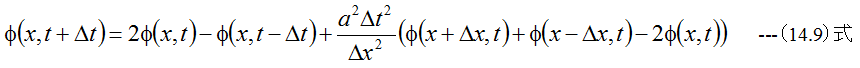
（14.9）式が得られます。（14.9）式によれば、Δｔ時間後のΦの値を次々と計算できることがわか ります。ただし（14.9）式が成立するためには、以下の条件式を満足するようにΔｔの値を設定する必要があります。
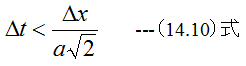
境界条件と（14.9）式、（14.10）式から1次元波動方程式を解くことができます。
1次元波動方程式.xls(フリーソフト)のダウンロード- ダウンロード
下記の1次元波動方程式.xls(フリーソフト)]をダウンロードしてください。
ダウンロード後はダブルクリックで解凍してから使用してください。
1次元波動方程式.xls(フリーソフト)]をダウンロードする。
- 1次元波動方程式.xls(フリーソフト)
- ファイル構成
（１） 1次元波動方程式.xls ：フリーソフトです。
（２）シート「Sheet1」：計算条件の設定と計算結果の出力を行います。
（２）シート「Sheet2」：計算結果をグラフ化します。
- 注意事項
（１）ファイルの保存場所の制限はありません。
- 標準的な実行方法
（１）「1次元波動方程式式.xls」をダブルクリックで起動します。
（マクロを有効にして開いてください！！）
（２）音速、音波周波数、発信波数、壁距離、距離の刻み回数、時間刻み、時間計算回数を設定します。
（３）その他の境界条件はプログラム内で自動設定されるため変更できません。
（４）「計算実行」ボタンを押します。
（５）計算結果がシート「Sheet1」に表示されます。
（６）設定できる距離の刻み回数制限があります。
プログラムリストVBAのプログラムリストは以下のようになります。
Dim F(256), OF(256), OF2(256)
Sub Main()
'初期入力
Pi = 3.141592654
A = Sheets("Sheet1").Cells(4, 3).Value
S = Sheets("Sheet1").Cells(5, 3).Value
Ns = Sheets("Sheet1").Cells(6, 3).Value
L = Sheets("Sheet1").Cells(7, 3).Value
Nl = Sheets("Sheet1").Cells(8, 3).Value
DX = Sheets("Sheet1").Cells(9, 3).Value
DT = Sheets("Sheet1").Cells(10, 3).Value
Nt = Sheets("Sheet1").Cells(11, 3).Value
C = (A ^ 2) * (DT ^ 2) / DX ^ 2
'初期設定
For i = 0 To Nl
F(i) = 0
OF(i) = 0
OF2(i) = 0
Next i
'表題出力
Sheets("Sheet1").Cells(15, 1).Formula = "時間(s)＼x(mm)"
For i = 0 To Nl
Sheets("Sheet1").Cells(15, 2 + i).Value = DX * i
Next i
'繰り返し計算
For j = 1 To Nt
T = DT * j
If T < Ns / S Then
F(0) = Sin(2 * Pi * S * T)
Else
F(0) = 0
End If
For i = 0 To Nl
OF2(i) = OF(i)
OF(i) = F(i)
Next i
For i = 1 To Nl - 1
F(i) = 2 * OF(i) - OF2(i) + C * (OF(i + 1) + OF(i - 1) - 2 * OF(i))
Next i
F(Nl) = 0
'結果出力
Sheets("Sheet1").Cells(15 + j, 1).Value = T
For i = 0 To Nl
Sheets("Sheet1").Cells(15 + j, 2 + i).Value = F(i)
Next i
Next j
End Sub
Sheets("Sheet2").Cells(5 + k, 1).Value = k
Sheets("Sheet2").Cells(5 + k, 2).Value = Se / Nk
If Se / Nk < e Then Exit For
Next k
'結果出力
Sheets("Sheet2").Cells(1, 1).Formula = "計算結果"
Sheets("Sheet2").Cells(4, 1).Formula = "計算回数"
Sheets("Sheet2").Cells(4, 2).Formula = "変化量"
For j = 0 To Nj - 1 Step 1
Sheets("Sheet2").Cells(4, 4 + j).Value = j
Next j
For i = 0 To Ni - 1 Step 1
Sheets("Sheet2").Cells(5 + i, 3).Value = i
For j = 0 To Nj - 1 Step 1
Sheets("Sheet2").Cells(5 + i, 4 + j).Value = T(i, j)
Next j
Next i
End Sub
サンプル条件の実行結果計算条件
| 項目 | 記号 | 値 | 単位 |
| 音速 | a | 343000 | ｍｍ/S |
| 音波周波数 | S | 30000 | Hz |
| 発信波数 | Ns | 1 | サイクル |
| 壁距離 | L | 30 | mm |
| 距離の刻み回数 | Nl | 25 | 回 |
| 距離刻み | ｄｘ | 1.2 | ｍｍ |
| 時間刻み | ｄｔ | 0.000001 | ｓ |
| 時間計算回数 | Nt | 800 | 回 |
計算結果グラフ
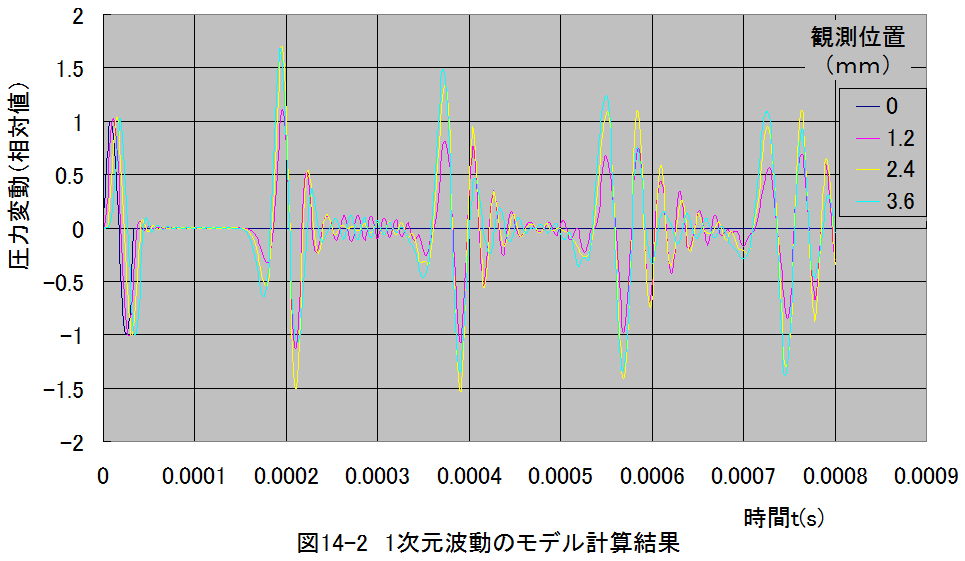
図14-2から発生した1サイクルの振動は音速で伝播し、各観測位置（1.2、2.4、3.6mm)に達することが理解 できます。また、振動は壁で反射し再度観測位置を通過後、音源で反射し再度観測位置を通過します。
なお、本モデルでは、振動の減衰を考慮していないため、壁と音源での反射が繰り返されます。
トラスの計算に行く。