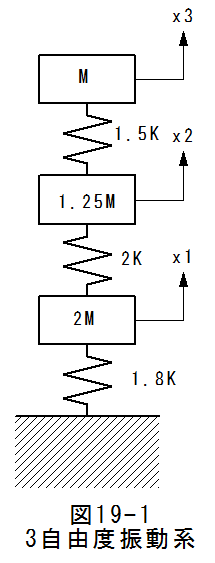
図19-1に示す3自由度振動系の固有振動数を求めます。この程度の振動系ならば手計算で簡単に解いてしまう方も多いと思います。しかし、4自由度、5自由度と自由度が増大するに従い手計算は困難となります。例題は3自由度ですが、自由度の増大を考慮した計算手法を検討します。
運動方程式図19-1に示す3自由度振動系の運動方程式は
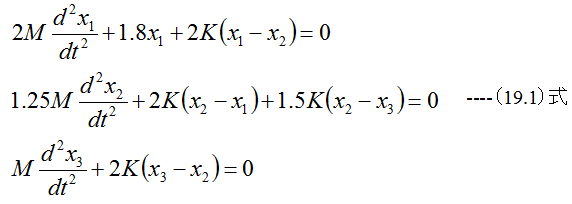
となります。（19.1）式は連立常微分方程式であり、ルンゲ・クッタ法で数値的に解くことも可能ですが、 今は固有振動数のみを知りたいとします。この場合
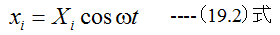
（19.1）式に（19.2）式を代入すると
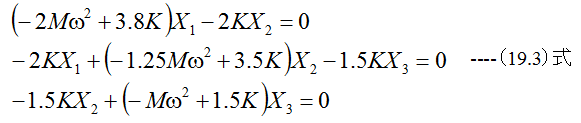
となります。
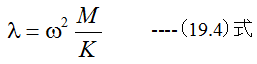
とするならば
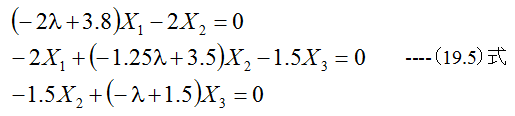
となります。λの係数を1にすると
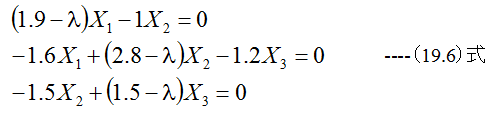
ここで（19.6）式は任意のX1,X2,X3について成立する必要があります。
ダニレフスキー法ここで行列式の定理を使用します。行列A=[aik]に対して
を満足するλおよび列ベクトルｘ≠[0]が存在するとき、λをAの固有値、ｘを固有 ベクトルといいます。これを単位ベクトルEを用いて式で表わすと
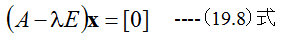
となります。この時ｘ≠[0]が存在する必要十分条件は
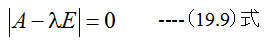
となります。この定理を（19.6）式に適用すると
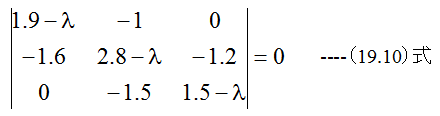
となります。（19.10）式は3次の行列式であり、手計算でも整理可能です。3次の方程式 であることは容易に理解できます。ここでは、一般化のためダニレフスキー法を使用します。
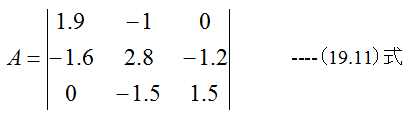
とおいて、
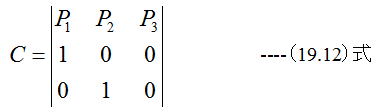
の形に変換します。そしてP1が高次方程式の2次の係数、P2が1次の係数、P3が0次の係数となります。
まず、行列A（19.11）式から正規行列Bｋをを作成します。
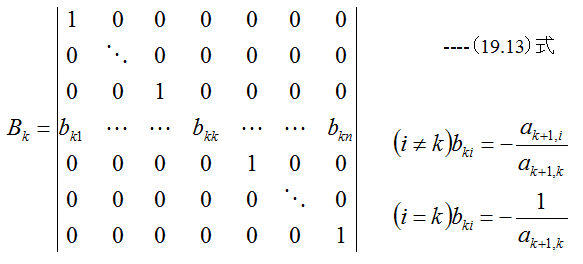
また、正規行列Bｋの逆行列は
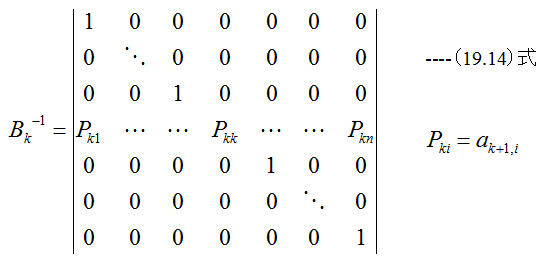
そして以下の計算を実行します。
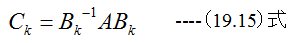
（19.15）式の計算をi,j,kについて１からnまで実行すると１回目の変換行列Cが求まります。この操作をｎ-1回繰り返すと（19.12）式の形式の行列に変化します。
何とも煩雑で難解なアルゴリズムですが、プログラム的には単純計算の繰り返しとなります。
最終的には、n次方程式に変換できますので「ベアストウ法」で解を求めます。
ダニレフスキー法実行結果ダニレフスキー法実行結果は以下のようになります。
| ダニレフスキー法計算回数=1 | |||
| * | j=1 | j=2 | j=3 |
| i=1 | 1.9 | 0.66667 | -1 |
| i=2 | 2.4 | 4.3 | -2.4 |
| i=3 | 0 | 1 | 0 |
| ダニレフスキー法計算回数=2 | |||
| * | j=1 | j=2 | j=3 |
| i=1 | 6.2 | -8.97 | 2.16 |
| i=2 | 1 | 0 | 0 |
| i=3 | 0 | 1 | 0 |
ベアストウ法実行結果ベアストウ法実行結果は以下のようになります。
| ベアストウ法計算回数=7 | ||
| * | 実数部 | 虚数部 |
| λ1 | 4.17576506721508 | 0 |
| λ2 | 0.3 | 0 |
| λ3 | 1.72423493278687 | 0 |
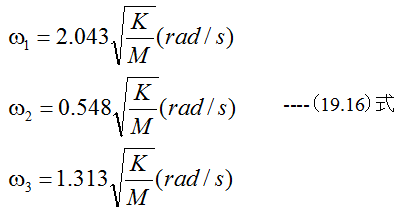
となります。虚数部がゼロでない場合、角速度ωは複素数となります。この場合どう判断するのか？少し疑問が残りま すが現実的な振動モデルでは実数解となります。
固有振動数.xls(フリーソフト)のダウンロード- ダウンロード
下記の固有振動数.xls(フリーソフト)]をダウンロードしてください。
ダウンロード後はダブルクリックで解凍してから使用してください。
固有振動数.xls(フリーソフト)]をダウンロードする。
- 固有振動数.xls(フリーソフト)
- ファイル構成
（１） 固有振動数.xls ：フリーソフトです。
（２）シート「Sheet1」：計算条件の設定を行います。
（３）シート「Sheet2」：ダニレフスキー法計算結果の出力を行います。
（4）シート「Sheet3」：ベアストウ法計算結果の出力を行います。
- 注意事項
（１）ファイルの保存場所の制限はありません。
- 標準的な実行方法
（１）「固有振動数.xls」をダブルクリックで起動します。
（マクロを有効にして開いてください！！）
（２）行列式の次数を設定します。
（３）固有値を求める行列を設定します。
（４）「計算実行」ボタンを押します。
（５）ダニレフスキー法計算結果がシート「Sheet2」に表示されます。
（６）ベアストウ法計算結果計算結果がシート「Sheet3」に表示されます。
・本プログラムはダニレフスキー法計算の様子を理解するため、各ステップごとの マトリックスの値を表示しています。このため、多くの変数、制約条件数の 計算にはてきしません。
、各ステップごとのマトリックスの値の表示をやめれば、多くの変数、制約条件数 に対応しやすくなります。
プログラムリストVBAのプログラムリストは以下のようになります。
'N=行列式の次数
'A(N,N)＝固有値を求める行列
'B(N,N)＝相似変換行列
'BINV(N,N)=相似変換の逆行列
'C(N,N)=相似変換後の行列
Dim A(51, 51), B(51, 51), C(51, 51), BINV(51, 51), RE(51), IM(51), N, Pn
Dim AA(51), BB(51), CC(51)
Dim M, PP, QQ, CT, ZZ, DP, DQ, EPS, ERR, EN
Sub Main()
Sheets("Sheet2").Cells.Clear
Sheets("Sheet3").Select
Sheets("Sheet3").Cells.Clear
N = Sheets("Sheet1").Cells(4, 3).Value
EN = 200 '演算回数制限値
EPS = 0.00000001 '誤差判定値
For i = 1 To N
For j = 1 To N
A(i, j) = Sheets("Sheet1").Cells(8 + i, 1 + j).Value
Next j
RE(i) = 0: IM(i) = 0
Next i
'ダニレフスキー法
DANILEVSKY
'ベアストウ法
BAIRSTOW
OUTPUT_B
End Sub
'ダニレフスキー法
Sub DANILEVSKY()
L = N - 1
Do
For i = 1 To N
For j = 1 To N
B(i, j) = 0: C(i, j) = 0: BINV(i, j) = 0
Next j
B(i, i) = 1: BINV(i, i) = 1
Next i
For j = 1 To N
B(L, j) = -A(L + 1, j) / A(L + 1, L)
Next j
B(L, L) = 1 / A(L + 1, L)
'反転処理
For j = 1 To N
BINV(L, j) = A(L + 1, j)
Next j
'AB積
For i = 1 To N
For j = 1 To N
PP = 0
For k = 1 To N
PP = PP + A(i, k) * B(k, j)
Next k
C(i, j) = PP
Next j
Next i
'BINV*C積
For i = 1 To N
For j = 1 To N
PP = 0
For k = 1 To N
PP = PP + BINV(i, k) * C(k, j)
Next k
A(i, j) = PP
Next j
Next i
Pn = N - L
OUTPUT_A
L = L - 1
Loop While L > 0
End Sub
'ベアストウ法
Sub BAIRSTOW()
For j = 1 To N
AA(j) = -A(1, j)
Next j
AA(0) = 1
M = N
Do Until M = 0
If M = 1 Then RE(M) = -AA(1): Exit Do
PP = 1: QQ = 1
CT = 0
A0 = AA(0)
For i = 0 To M
AA(i) = AA(i) / A0
Next i
If M = 2 Then
PP = AA(1): QQ = AA(2)
Else
REPEAT
End If
QUADRATIC
M = M - 2
For i = 1 To M
AA(i) = BB(i)
Next i
Loop
End Sub
Sub REPEAT()
Do
CT = CT + 1
BB(0) = 1
BB(1) = AA(1) - PP
BB(2) = AA(2) - PP * BB(1) - QQ
For j = 3 To M
BB(j) = AA(j) - PP * BB(j - 1) - QQ * BB(j - 2)
Next j
CC(0) = 1
CC(1) = BB(1) - PP
CC(2) = BB(2) - PP * CC(1) - QQ
For j = 3 To M - 1
CC(j) = BB(j) - PP * CC(j - 1) - QQ * CC(j - 2)
Next j
ZZ = CC(M - 2) ^ 2 - CC(M - 3) * (CC(M - 1) - BB(M - 1))
DP = (CC(M - 2) * BB(M - 1) - CC(M - 3) * BB(M)) / ZZ
DQ = (CC(M - 2) * BB(M) - BB(M - 1) * (CC(M - 1) - BB(M - 1) - BB(M - 1))) / ZZ
PP = PP + DP: QQ = QQ + DQ
If CT > EN Then ERR = 1: Exit Do
Loop Until Abs(DP) < EPS And Abs(DQ) < EPS
End Sub
Sub QUADRATIC()
DD = PP ^ 2 - 4 * QQ
B1 = -0.5 * PP
B2 = Sqr(Abs(DD)) * 0.5
RE(M) = B1: RE(M - 1) = B1
If DD <= 0 Then
IM(M) = B2: IM(M - 1) = -B2
Else
If PP > 0 Then B2 = -B2
RE(M) = B1 + B2
RE(M - 1) = QQ / RE(M)
End If
End Sub
Sub OUTPUT_A()
Sheets("Sheet2").Cells(1 + 10 * (Pn - 1), 1).Formula = "ダニレフスキー法計算回数=" & Pn
For j = 1 To N
Sheets("Sheet2").Cells(1 + 10 * (Pn - 1) + 1, j + 1).Formula = "j=" & j
Next j
For i = 1 To N
Sheets("Sheet2").Cells(1 + 10 * (Pn - 1) + i + 1, 1).Formula = "i=" & i
For j = 1 To N
Sheets("Sheet2").Cells(1 + 10 * (Pn - 1) + i + 1, j + 1).Value = A(i, j)
Next j
Next i
End Sub
Sub OUTPUT_B()
Sheets("Sheet3").Cells(1, 1).Formula = "ベアストウ法計算回数=" & CT
If ERR = 1 Then
Sheets("Sheet3").Cells(13, 6).Formula = "エラー"
Else
Sheets("Sheet3").Cells(2, 2).Formula = "実数部"
Sheets("Sheet3").Cells(2, 3).Formula = "虚数部"
For i = 1 To N
Sheets("Sheet3").Cells(2 + i, 1).Formula = "λ" & i
Sheets("Sheet3").Cells(2 + i, 2).Value = RE(i)
Sheets("Sheet3").Cells(2 + i, 3).Value = IM(i)
Next i
End If
End Sub
上記プログラムの多くの部分はベアストウ法の記載であり、ダニレフスキー法の記載は少ないことがわかります。
２０章：座標の同時変換に行く。