最小自乗法による関数近似一般論区間X1〜X2において、真値を与える関数を
Y=F(X) ---（2.1）
とする。
近似式を
Z=P(X) ---（2.2）
とする。
（2.1）式と（2.2）式の誤差関数を下記で定義する。
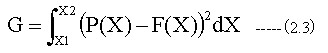
誤差関数（2.3）式の値が最小となるように近似式Z=P(X) を決定する方法を最小自乗法による関数近似という。
真値が連続関数でなく、m個の離散データYiで与えられるとき誤差関数は下記となる。
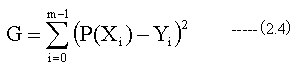
（2.4）式はデータの重みが均一の場合であるが、均一でない場合は重み関数をかける場合がある。
最小自乗法による多項式近似近似式Z=P(X)は任意の関数形であるが、実際には具体的な関数形を定義する必要がある。
具体的な関数形としては下記の多項式を考える。
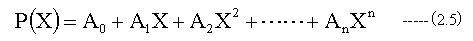
（2.5）式の定数A0〜Anは下記のn+1個の条件式を満足するように決定します。
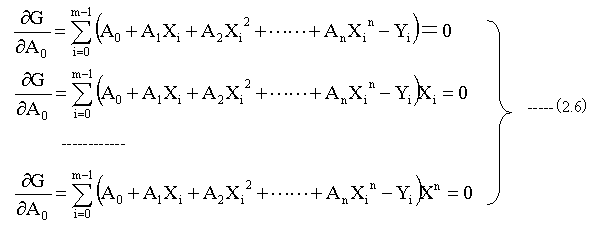
(2.6)式は以下のように変形されます。
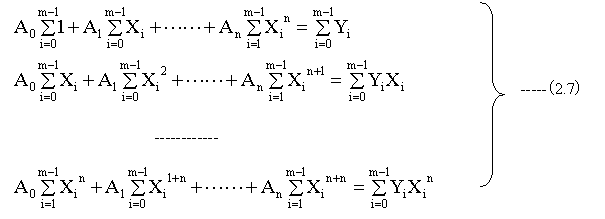
（2.7）式において未知数はA0〜Anのn+1個であり、連立方程式を解くことにより、n次多項式の係数を求めることができます。
２章：VBAのプログラムリストに行く。