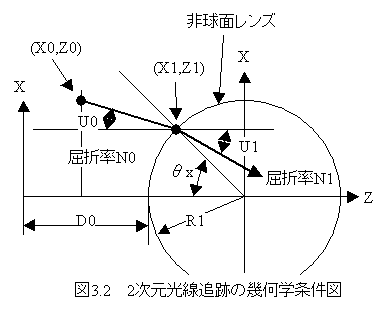
非球面レンズの2次元光線追跡の関係式非球面レンズに関しては、2次元の計算で十分の場合が多い。まず、 2次元光線追跡の計算式を導く。
- 入力パラメータ
図3.2の幾何学条件図において入力パラメータは 下記のとおりである。
Z0：入射光光軸方向座標
X0：入射光像高X方向座標
U0：入射光のX方向角度
R1：レンズ面の曲率半径
D0：レンズ面の光軸方向距離
Ox1：レンズX方向オフセット
N0：入射側の屈折率
N1：出射側の屈折率
- 中間パラメータ
θx：レンズ面法線のX方向角度
- 出力パラメータ
Z1：出射光光軸方向座標
X1：出射光像高X方向座標
U1：出射光のX方向角度
- 関係式
入射光の直線の方程式から
X1=X0 - (tan(U0))*(Z1 - Z0) -------(3.2)式
非球面方程式から Z1=F(X1-Ox1)+D0 -------(3.3)式
屈折の法則から
N0*SIN(θx - U0) = N1*SIN(θx - U1) -------(3.4)式
法線の条件から
TAN(θx）= ΔZ1/ΔX1 -------(3.5)式
以上の関係式が成立する。
未知数が中間パラメータ(θx)、出力パラメータ(Z1,X1,U1)の4個に対して、関係式が4個成立 する。
従って、(3.2)(3.3)(3.4)(3.5)式の関係から出力パラメータ(Z1,X1,U1)を求めることができる。
- 関係式の解を求める
(3.2)式と(3.3)式からX1とZ1の解を求めます。
(3.2)式に(3.3)式を代入し変形すると
G(X1)=X1-X0+Tan(U0)*(F(X1-Ox1)+D0-Z0)=0 -------(3.6)式
(3.6)式は代数的に解くのが難しいのでニュートン法で解を求めます。
「特設講座」有能エンジニアのための実用数値計算
１章：ニュートン法により代数方程式の解を求める
を参照しましょう。
Java Scriptで表現すると
N=10; dX=0.05;
for(i=0;i < N;i++) x=x-G(x)*2*dX/(G(x+dX)-G(x-dX));
でG(x)=0の解X1を求めることができます。
(3.5)式のΔZ1/ΔX1は数値微分で求めます。
X1は既に求まっています。従って
Z1=F(X1-Ox1)+D0 -------(3.3)式
θx=ATAN(ΔZ1/ΔX1) -------(3.7)式
U1 =θx -ASIN((N0/ N1)*SIN(θx - U0)) -------(3.8)式
から屈折後の光線を求めることが出来ます。
垂直平面の2次元光線追跡の関係式入射光の直線の方程式から
X1=X0 - (tan(U0))*(Z1 - Z0) -------(3.2)式
垂直平面方程式から Z1=D0 -------(3.9)式
屈折の法則から
N0*SIN(θx - U0) = N1*SIN(θx - U1) -------(3.4)式
法線の条件から
TAN(θx）=0 -------(3.5)式
と単純な計算式となります。