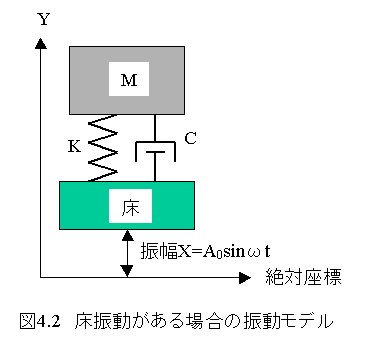
床振動の運動方程式床振動がある場合の振動モデルを図4.2に示します。
図4.2において、床は
X=A0sin(ωt）
で振動しているとします。
従って、床の速度は
X'=A0ωcos(ωt）
床の加速度は
X''=-A0ω2sin(ωt）
ということになります。
ここで、床の変位はバネKを通じて質量Mに伝達します。
また、床の速度X'は粘性抵抗Cを通じて質量Mに伝達します。
しかし、床の加速度X''は質量Mに伝達しません。
質量Mに対する加速度は絶対座標系における加速度が適用されます。
ここで、絶対座標系とは何か？という問題が発生します。
地球は太陽を中心として公転しています。また、地球は自転しています。 床は地表の上に設置されています。
まず、公転は一定速度で運動しており、加速度の変化は無視できるとします。
次に自転ですが、自転も一定速度で運動しており、加速度の変化は無視できるとします。
さて、火山の爆発等による地震の影響ですがこれは、加速度の変化を伴うため、無視できません。
従って、絶対座標は地球の中心を基準にとれば、加速度の変化の影響を無視できると仮定できます。
以上の考察から、床振動がある場合の運動方程式は以下となります。
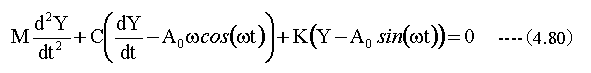
（4.80）式の微分方程式の解N元の連立微分方程式にあてはめるため、下記式のように変形します。
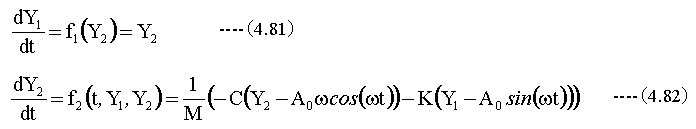
(4.70)式と（4.71）式をN元の連立微分方程式にあてはめると以下のようになります。
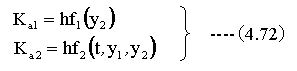
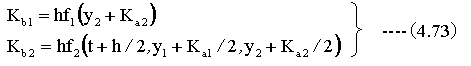
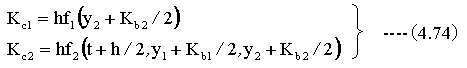
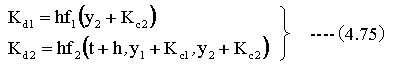
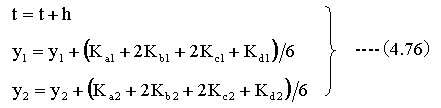
以上の計算を繰り返すことにより、微分方程式の解を求めることができます。
以上のような単純計算を繰り返すことにより、微分方程式の解が求まるのはマジック のようですが、確認は実際に計算してみるのが一番です。
５章：VBAによるN元の連立微分方程式プログラムリストに行く。