N元の連立微分方程式フリーソフトのダウンロード下記の[N元の連立微分方程式フリーソフト]をダウンロードしてください。
ダウンロード後はダブルクリックで解凍してから使用してください。
[N元の連立微分方程式フリーソフト]をダウンロードする。N元の連立微分方程式フリーソフト説明- ファイル構成
（１）微分方程式1.xls ：加振力がある場合の振動モデル設定例です。
（２）微分方程式2.xls ：床振動がある場合の振動モデル設定例です。
- 注意事項
注（１）ファイルの保存場所の制限はありません。
- 標準的な実行方法
（１）「微分方程式1.xls」または「微分方程式2.xls」をダブルクリックで起動します。
（マクロを有効にして開いてください！！）
（２）黄色のセルに値を設定します。
（３）「計算実行」ボタンを押します。
（４）計算結果が表示されます。
加振力がある場合の振動モデル設定の説明- 計算式は下記です。
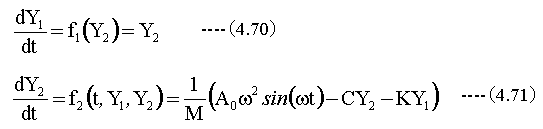
- 連立数n＝2です。
- 時間刻みh=0.01sです。（この値は振動周波数を25Hzとした場合、1/（4×25）＝0.01s以下でなければなりません。）
- 計算回数Nc=200としました。
- 質量M=100kgとしました。
- 粘性係数は臨界粘性係数の1/10である125.7kg/sとしました。
- バネ定数は固有振動数が1Hzとなる3948kg/s2としました。
- 加振力振幅A0=9.8kgm/s2としました。
- 角速度は25Hz=157.1rad/sとしました。
- 初期時間ｔ＝0sとしました。
- 初期変位ｙ1＝0mとしました。
- 初期速度ｙ2＝0m/sとしました。
- f1=F12としました。
- f2=(J13*SIN(J14*F10)-J11*F12-J12*F11)/J10としました。
「計算実行」ボタンを押すと計算が実行されます。
加振力がある場合の振動モデル設定の計算結果シート「Graph1」には下記のグラフが表示されます。
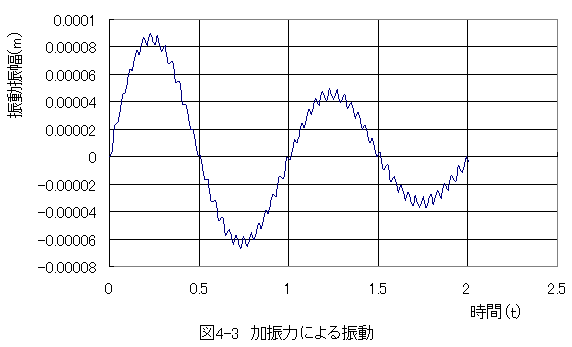
細かな振動が加振力（25Hz)による振動です。
大きな振動が固有振動起因の振動です。
バネ定数を大きくすると加振力（25Hz)による振動が大きくなります。
（パラメータを変えて計算することにより、パラメータの影響がわかります。）
床振動がある場合の振動モデル設定の説明- 計算式は下記です。
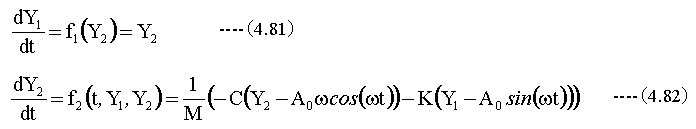
- 連立数n＝2です。
- 時間刻みh=0.01sです。（この値は振動周波数を25Hzとした場合、1/（4×25）＝0.01s以下でなければなりません。）
- 計算回数Nc=200としました。
- 質量M=100kgとしました。
- 粘性係数は臨界粘性係数の1/10である125.7kg/sとしました。
- バネ定数は固有振動数が1Hzとなる3948kg/s2としました。
- 床振動振幅A0=0.0001mとしました。
- 角速度は25Hz=157.1rad/sとしました。
- 初期時間ｔ＝0sとしました。
- 初期変位ｙ1＝0mとしました。
- 初期速度ｙ2＝0m/sとしました。
- f1=F12としました。
- f2=(-J11*F12-J12*((F11-J13*J14*COS(J14*F10))-J13*SIN(J14*F10)))/J10としました。
「計算実行」ボタンを押すと計算が実行されます。
床振動がある場合の振動モデルの計算結果シート「Graph1」には下記のグラフが表示されます。
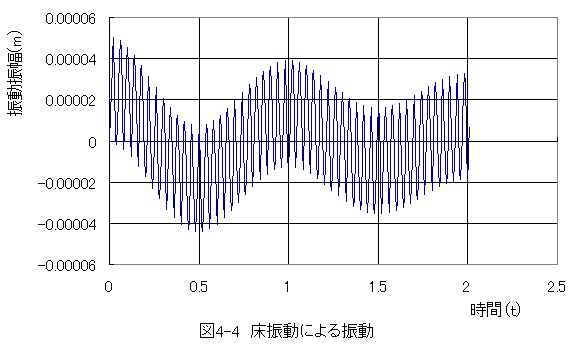
細かな振動が加振力（25Hz)による振動です。
大きな振動が固有振動起因の振動です。
床振動の振幅が100μｍに対して、質量Mの振動振幅は約20μｍ程度と約1/5になっていることがわかります。
質量Mを大きくしたり、バネ定数Kを小さくすると防振効果が大きくなります。
（パラメータを変えて計算することにより、パラメータの影響がわかります。）
振動と微分方程式のまとめ- 振動問題はさまざまな振動形態があり、また、時間的にも変化するため完全に解析することは困難です。
- したがって、振動対策は安全率を十分とって行う必要があります。
- 振動対策の基本はベース質量の増大とバネ定数の縮小ですが、床強度が制限事項になります。
- 微分方程式の解を求める方法としては、ラプラス変換・ラプラス逆変換法が最も精度の良い解を
得ることができますが、式の変換は結構やっかいな作業となります。
- 連立ルンゲ・クッタ法を用いると、式の変換は驚くほど簡単になります。
- N元の連立微分方程式フリーソフトを使用すると、10元までの任意の線形微分方程式を
プログラム変更なしに設定変更のみで解くことができます。
トップページに戻る。