プログラミングの課題より大きなデータ数Nに対する高速FFTが可能なことがわかりましたが、プログラミング上の課題が残っています。
課題1
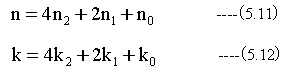
(5.28)式、(5.29)式を一般化して扱うのは、プログラミング的に扱うのは難しく工夫が必要です。
課題2
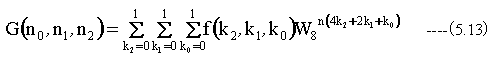
（5.13）式で示されているように、元の関数ｆ(k)とFFT変換後の関数G(n)で2進数の桁の順序が逆転しています。
従って、ビットの逆転をした並び替えが必要となります。
以上の課題はプログラミングのテクニック上の課題となります。
データ数N=8の場合の回転子演算プログラム例データ数N=8の場合の回転子演算プログラムのC言語記載例を下記に示します。
#include
void main()
{
int i,ns,L1,n,arg,arg2,i0,i1,m[100],L,n1;
L=3;//2進数のビット数
n=(int)pow(2,L);//データ数
n1=n/2;//データ数の1/2
ns=n/2;//2進数の最上位の値
for(i=0; i < n; i++){m[i]=0;} //m[i]の初期化
while(ns >= 1) //2進数の最上位の値が1になるまで繰り返し
{
for(L1=0;L1 < n;L1=L1+2*ns) //L1の値を0からnまで、2×最上位の値のstepで繰り返し
{
arg=m[L1]/2;//回転子=前の回転子の値/2
arg2=arg+n1;//回転子2＝回転子+データ数の1/2
for(i0=L1; i0 < L1+ns; i0++) //i0の値をL1の値からL1+2進数の最上位の値まで繰り返し
{
i1=i0+ns;//i1＝i0+2進数の最上位の値
m[i0]=arg;//m[i0]に回転子を保存
m[i1]=arg2;//m[i1]に回転子2を保存
}
}
ns=ns/2;//2進数の最上位の値を繰り下げ
}
}
上記のプログラムを実行すると各計算ステップ毎に、回転子の値がm[i]に記録されます。
しかし、直感的には、どのような回転子の値がm[i]に記録されるかを予想するのが難しいプログラムです。
サンプルプログラム変数の変化データ数N=8の場合の回転子演算プログラム実行結果を下記表に示します。
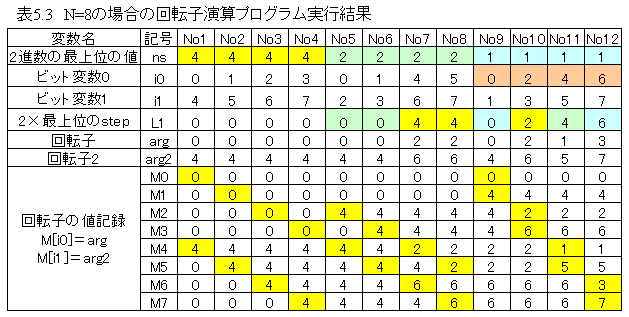
表5.3 N=8の場合の回転子演算プログラム実行結果において、
1 2進数の最上位の値（ns)は4→2→1の3段階で変化します。
2 ビット変数（i0）は、各段階毎にL1の値からL1+2進数の最上位の値まで変化します。
3 ビット変数（i1）は、 i1＝ i0+nsです。
4 2×最上位のstep(L1)は、各段階毎にL1の値を0からnまで、2×最上位の値のstepで変化します。
5 回転子の値記録は各計算ステップ毎に2個づつ記録されていきます。（黄色のセル）
6 回転子の値記録が最終的に完了するとM[i]には配列順のビット反転をした数値が記録されています。
以上が実行結果ですが、巧妙に回転子の値が変化していく様子がわかります。
最後には、ビット反転データがM[i]に残りますにで、この値を使ってビット反転処理を行うことができます。
３章：高速フーリエ変換プログラムのC言語ソースに行く。