偏微分方程式の解（例１）下記に示すような多変数の関数は、微分すると偏微分となります。
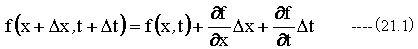
（下記に示す偏微分方程式が与えられた時の解f(x,t)を求める。
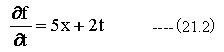
t＝0の時の初期条件を下記とする。
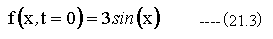
（21.2）式をラプラス変換すると
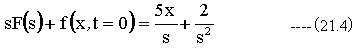
(21.3)式の初期条件を（21.4）式に代入して整理すると
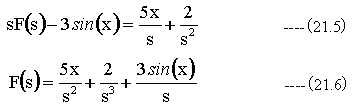
逆変換をおこなうと
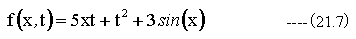
となる。
偏微分方程式の解（例２）下記に示す偏微分方程式が与えられた時の解f(x,t)を求める。
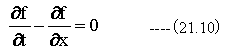
初期条件は下記とする
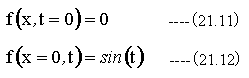
(21.10)式をラプラス変換すると
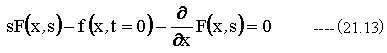
（21.11）式を代入して整理すると
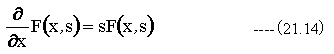
（21.14）式は微分して関数形が変化しないので、下記の指数関数が解となる。
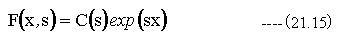
（21.15）式において、C(s)はｓの関数である。
Ｘ＝0とすると（21.15）式は
従って
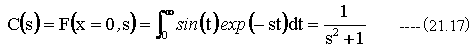
よって
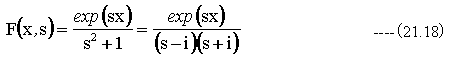
逆変換は
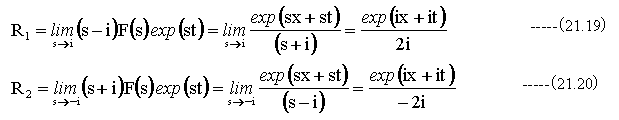
従って
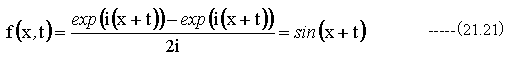
となります。
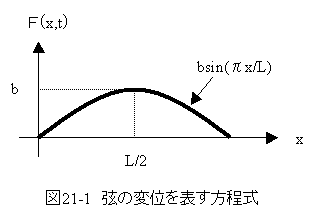
偏微分方程式の解（例３）図21-1に示す弦の変位を表す方程式は下記の偏微分方程式となります。
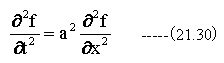
境界条件
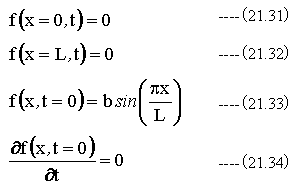
（21.30）式をラプラス変換すると
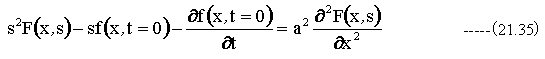
境界条件をいれると
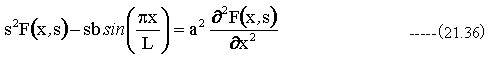
(21.36)式は下記のように書き換えることができる。
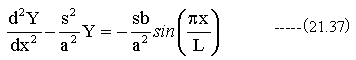
ここで下記式の特殊解を求めます。
ここで
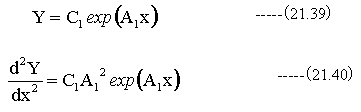
（21.38）式に（21.39）式と（21.40）式を代入して整理すれば、
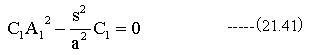
従って
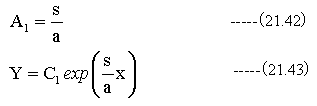
同様にして
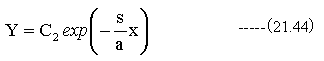
も特殊解となります。
最後の特殊解は下記式を代入して求めます。
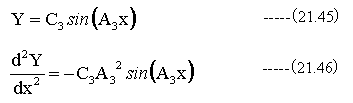
（21.37）式に（21.45）式と（21.46）式を代入して
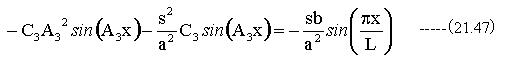
従って
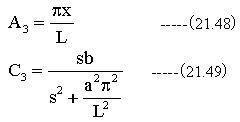
従って
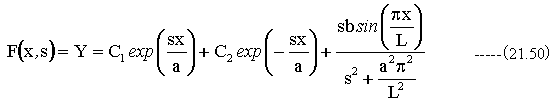
境界条件
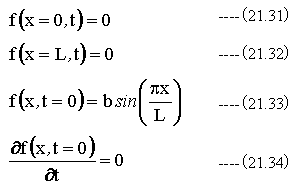
から
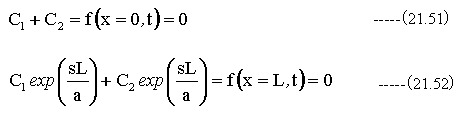
（21.51）式と（21.52）式を満足する定数は
従って
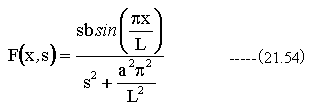
（21.54）式をラプラス逆変換すると
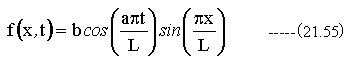
これが求める解である。
（21.55）式において、aが大きく、弦の長さが短いほど高周波振動となる。
後書き複素数や複素関数は概念的に理解しにくいですが、2次以上の方程式を解くために 複素数が必要となります。
また、微分方程式を解くために複素関数が必要となります。
そして、ラプラス変換・ラプラス逆変換を使用すると、微分方程式を鮮やかに解くことが できます。
偏微分方程式の解においては、ラプラス変換・ラプラス逆変換法と代入法を併用して 解を求めていますが、代入法と比較してラプラス変換・ラプラス逆変換法は鮮やかです。
トップページに戻る。