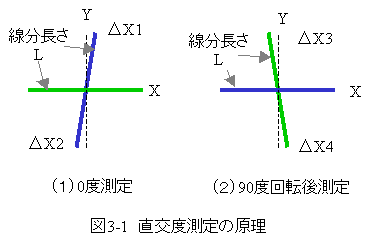
直交度図3-1に直交度測定の原理を示します。
図3-1の（１）0度測定において、緑と青の線分の長さはLで、緑の線分をX軸に一致させてあります。
このとき、パターンに直交度誤差があると理想位置からΔX1、 ΔX2だけずれを生じます。
直交度誤差は
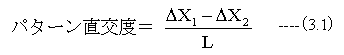
となります。次にパターンを90度正方向に回転して測定すると、図3-1の（２）90度回転後測定のようになります。
90度回転後は青の線分をX軸に一致させます。
このときの直交度は
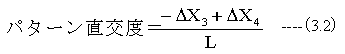
となります。（3.1）式と（3.2）式の平均直交度は
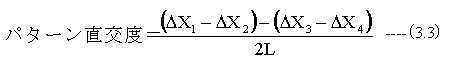
となります。ここで、測定機の直交度誤差がゼロの場合
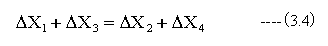
が成立します。測定機の直交度誤差がある場合は（3.4）式が成立しなくなります。
測定機の直交度誤差は
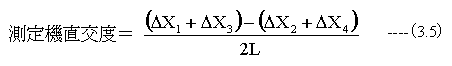
となります。
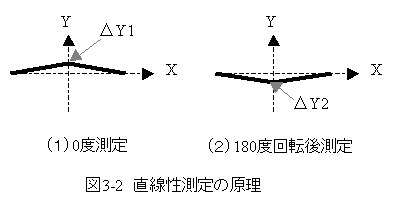
直線性図3-2に直線性測定の原理を示します。
図3-2の（１）0度測定において、3点は等間隔で、両端の2点をX軸に一致させてあります。
このとき、直線性誤差があると理想位置からΔY1だけずれを生じます。
次にパターンを180度回転して測定すると、図3-2の（２）180度回転後測定のようになります。
両端の2点をX軸に一致させます。
このときの誤差をΔY2とします。
パターンの直線性誤差は
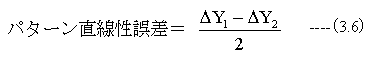
となります。ここで、測定機の直線性誤差がゼロの場合
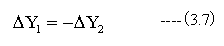
が成立します。測定機の直線性誤差がある場合は（3.7）式が成立しなくなります。
測定機の直線性誤差は
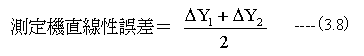
となります。
回転格子法位置精度の検証用のパターンは通常等ピッチで配置された格子パターンを用います。しかし検証用のパターンを誤差ゼロで作成することは困難です。
位置誤差のある検証用パターンで精度良く位置の検証を行う場合に回転格子法は有効です。
（１）回転格子法の原理
回転格子法では、等ピッチで格子状に配置されたパターンを0度、90度、180度、270度回転した測定データに基づいて、測定機誤差とパターン誤差を算出します。
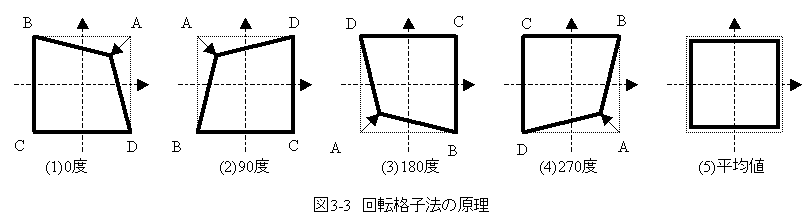
図3-3に回転格子法の原理を示します。図3-3において、格子パターンは単純な4点の格子としています。4点A,B,C,DのうちA点のみ誤差がある図を示ています。
このパターンを0度、90度、180度、270度回転した測定データの平均値を求めると正確な正方形になることがわかります。もし、この0度、90度、180度、270度回転の平均値が正方形からずれていたら、それは測定機誤差となります。
次にパターン誤差ですが、 0度、90度、180度、270度回転測定データを回転した分元に戻して平均値を求めます。この場合、測定機の誤差がキャンセルされて純粋なパターン誤差となります。
以上が回転格子法の原理ですが、樽型歪、糸巻き歪等の回転対称な誤差成分は除去できません。この場合は回転中心をずらして測定を行う必要が生じます。
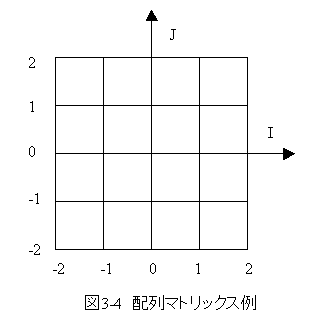
５×５回転格子法例図3-4に配列マトリックス例をしめします。
（１）測定機誤差
測定機誤差は0度測定時の誤差をX0（I,J) Y0（I,J) 、90度測定時の誤差をX90（I,J)Y90（I,J) 、180度測定時の誤差をX180（I,J) Y180（I,J)、270度測定時の誤差をX270（I,J) Y270（I,J)とすれば、単純平均として求めることができます。
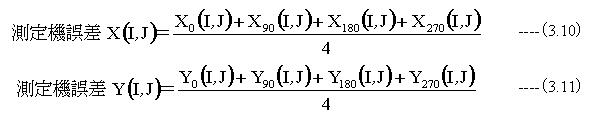
（3.10）式、（3.11）式において、I,Jは格子位置を示します。
（２）パターン誤差パターン誤差は回転を元に戻してから平均値を計算する必要があります。
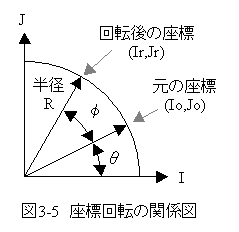
図3-5に座標回転の関係図を示します。
回転後の座標は
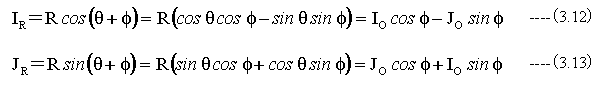
（3.12）式と（3.13）式から回転による座標変換は下記表のようになります。
誤差ベクトルの方向も同様に回転の影響を受けます。
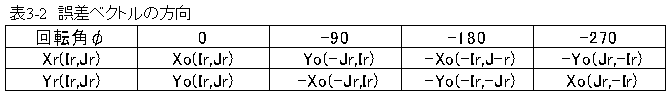
したがって、パターン誤差は
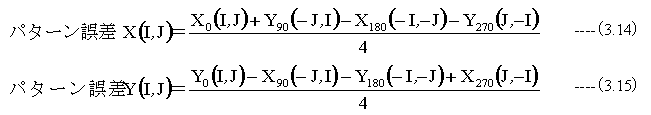
となります。
５×５回転格子法の実例下記のサンプルプログラム「回転格子法.xls」をダンロード願います。
ワークブック「回転格子法.xls」をダウンロードする。ダウンロード後はダブルクリックで解凍してから使用してください。
サンプルプログラムには、下記表の測定データが入力してあります。
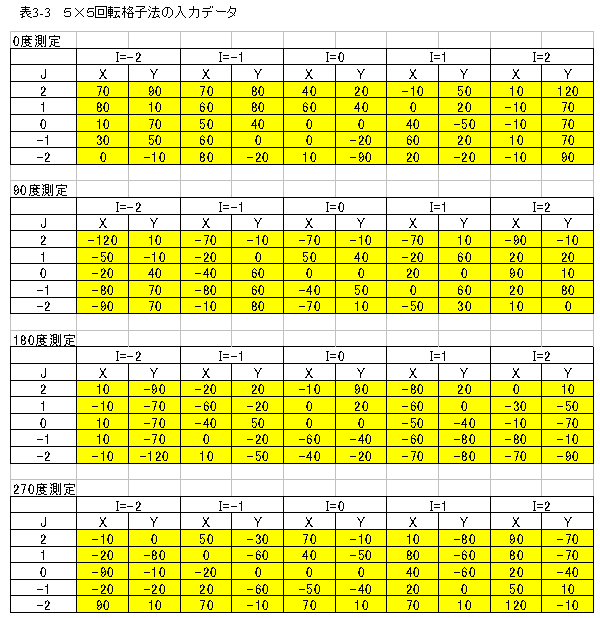
90度測定、180度測定、270度測定データは、0度測定の値を単純に回転処理して作成したデータです。
「計算実行」ボタンを押すと「測定機誤差」と「パターン誤差」が計算されます。
ここで、 「パターン誤差」は「 0度測定データ」と完全に一致します。単純に回転処理して作成したデータを元の回転位置に変換して、平均を求めたため当然の結果です。
本来、この条件において「測定機誤差」は全てゼロになるべきです。しかし、 「測定機誤差」はゼロとなりません。回転格子法においては、 「パターン誤差」の影響が残ってしまうのです。
しかし、 「測定機誤差」は「パターン誤差」より小さな値となります。従って、回転格子法を用いない場合と比較するならば、誤差は低減します。
厳密な精度管理より厳密な精度管理を行うには、非常に熱膨張係数の小さい基板で複数枚のサブ原器パターンを作成し、多くの測定機で「パターン誤差」を求める必要があります。
多くの測定機で「パターン誤差」を求め、平均処理を行うとより真値に近い「パターン誤差」を求めることができます。
真値に近い「パターン誤差」を求め補正することにより、より厳密な測定が可能となります。従って、一つのサブ原器パターンを繰り返し測定し、平均化処理により誤差を少なくしていぐことが可能です。
あとがき原子時計の出現により、極めて高い精度で時間を計測することが可能となりました。さらには、ドップラー効果型のレーザ測長機の出現により、高い精度で光速を測定可能となりました。 そして、真空中の光速度を基準にメートル原器が制定されました。これにより、長寸法を高い精度で測定することが可能となりました。 2次元的な座標は直角と直線で定義されます。 2次元的な座標を検定する方法として、回転格子法は有効な手段です。しかし、回転格子法は完全な手法ではなく、補正値の使用が必要となります。 回転格子法とより厳密な補正値管理により、高精度な位置計測が可能となります。
トップページに戻る。