「キットで遊ぼう電子回路 No.10 ６石AMラジオ編」原理解説テキストの【原理解説編】で詳細の解説があります。
直列発振回路と並列発振回路直列発振回路を図4-1、並列発振回を図4-2に示します。
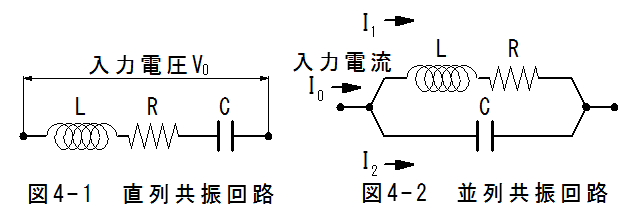
直列発振回路では回路の両端に入力電圧V0を加えて駆動します。この場合の関係式は
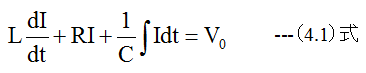
となります。並列発振回では入力電流I0を流して駆動します。この場合の関係式は
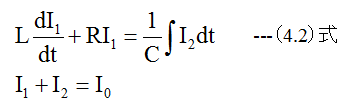
となります。（4.2）式を変形すると
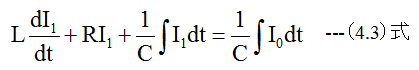
となり、（2.1）式と（2.3）式は入力電圧か入力電流かの違いのみで、同じ形の微分方程式となります。回路の固有振動数は入力電圧ま たは、入力電流が無い場合の自由振動数であり、直列発振回路と並列発振回路は同じ計算式となります。
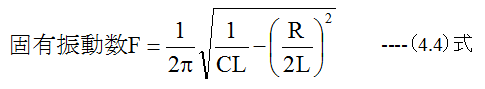
バーアンテナ共振回路の共振周波数課題
バーアンテナの1次側インダクタンスはL=800μH、直流抵抗はR=5.6Ωです。共振周波数が594kHzとなるバリコンの容量Cは何ｐFか？
（１）直流抵抗R=0Ωとし
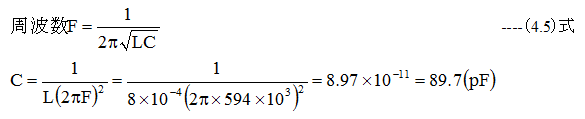
（２）直流抵抗R=5.6Ωとした場合
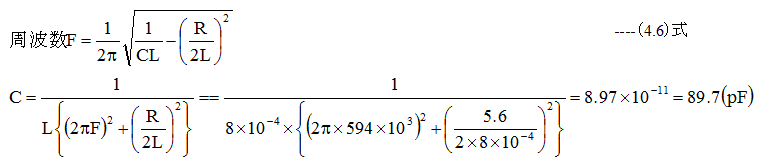
(4.5)式と(4.6)式は異なるのですが、直流抵抗R=5.6Ωは計算上の誤差に埋もれてしまいほぼ同じ値になります。
バーアンテナ共振回路の信号波形の計算計算とグラフ化の都合で594ｋHz(NHK)に10kHzの音声をのせた入力信号とします。数値計算（ルンゲクッタ法）で計算しました。
計算結果グラフを図4-3に示します。
計算条件
*インダクタンスはL=800μH
*直流抵抗はR=5.6Ω
*バリコンの容量C＝89.7ｐF
*電波周波数＝594kHz
*音声周波数＝10ｋHz
*計算時間間隔＝0.1μｓ
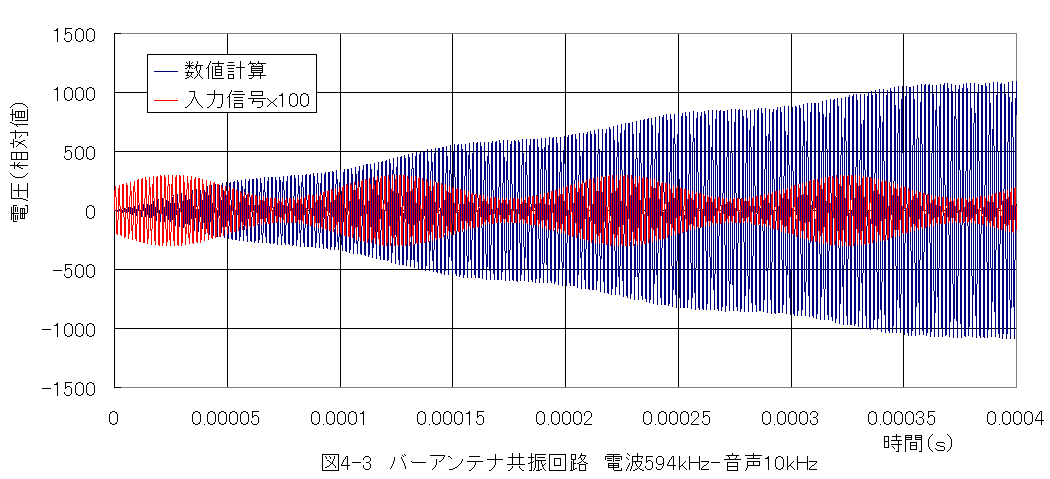
*数値計算の都合で時間ｔ＝0以前は信号ゼロとなっています。
*入力信号に対して、共振後の信号が数百倍となります。
*入力信号は100倍して表示しました。
局部発振回路課題
局部発振回路インダクタンスはL=800μH、直流抵抗はR=0Ωとした場合、共振周波数が694kHz（＝594ｋHz+100kHz)となるコンデンサの容量Cは何ｐFか？
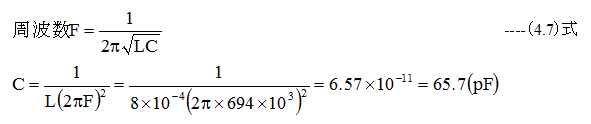
局部発振回路の信号波形の計算計算とグラフ化の都合で594ｋHz(NHK)に10kHzの音声をのせた入力信号とします。うなりは100ｋHzとしました。数値計算（ルンゲクッタ法）で計算しました。
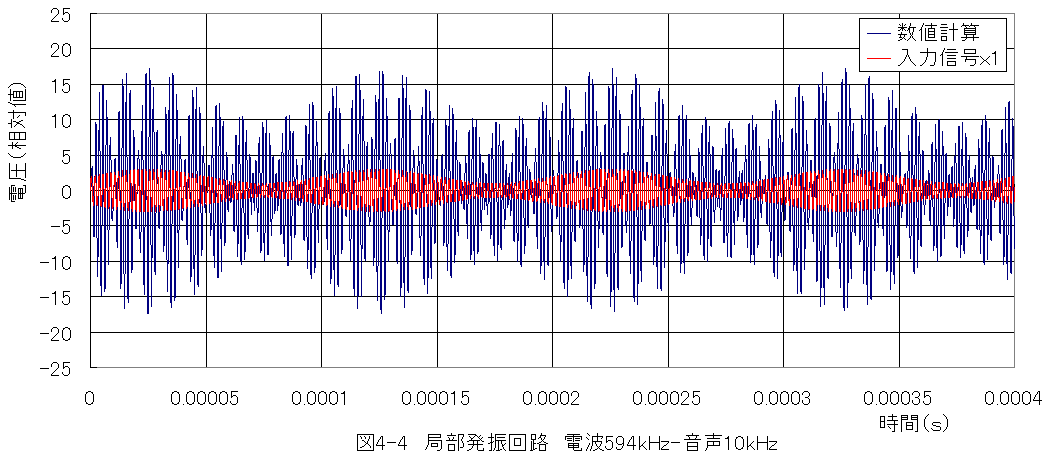
計算結果グラフを図4-4に示します。
計算条件
*インダクタンスはL=800μH
*直流抵抗はR=0Ω
*容量C＝65.7ｐF
*電波周波数＝594kHz
*音声周波数＝10ｋHz
*計算時間間隔＝0.1μｓ
*数値計算の都合で時間ｔ＝0以前は信号ゼロとなっています。
*入力信号に対して、共振後の信号が数倍となります。
*入力信号は1倍で表示しました。
*100kHzのうなりが発生することが確認できます。
中間周波数共振回路課題
局部発振回路インダクタンスはL=800μH、直流抵抗はR=0Ωとした場合、共振周波数が100kHz)となるコンデンサの容量Cは何ｐFか？
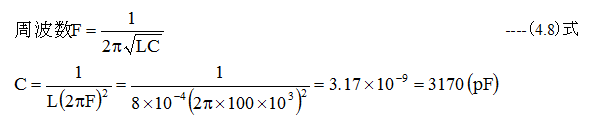
中間周波数共振回路の信号波形の計算計算とグラフ化の都合で594ｋHz(NHK)に10kHzの音声をのせた入力信号とします。うなりは100ｋHzとしました。数値計算（ルンゲクッタ法）で計算しました。
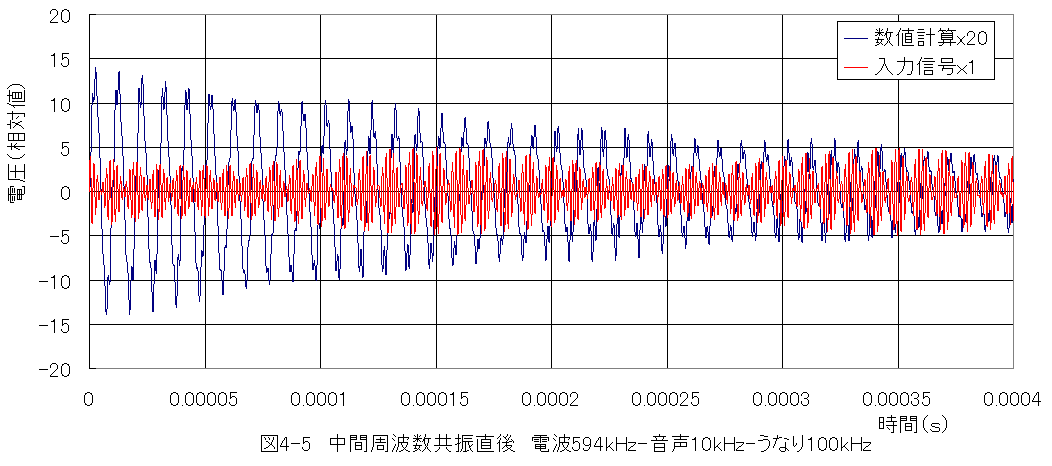
計算結果グラフを図4-5に示します。
計算条件
*インダクタンスはL=800μH
*直流抵抗はR=0Ω
*容量C＝3170ｐF
*電波周波数＝594kHz
*うなり周波数＝100kHz
*音声周波数＝10ｋHz
*計算時間間隔＝0.1μｓ
*数値計算の都合で時間ｔ＝0以前は信号ゼロとなっています。
*入力信号に対して、共振後の信号が1/20倍となります。
*出力信号は20倍で表示しました。
*100kHzに音声がのった信号が確認できます。
*入力信号に対して、共振後の信号が1/20倍と小さくなりますが、うなりの周波数成分のみを抽出可能であることが理解できます。
結果の検討（１）LとCで構成される共振回路の特性を線形微分方程式の数学モデルに置き換え、その特性を検討しました。
（２）計算条件として、実際の周波数を適用すると計算とグラフ化が面倒なので、電波周波数594kHzに対して、音声10kHz、うなり周波数（中間周波数）100kHzとしました。
（３）共振回路の固有振動数と入力信号の周波数が一致する場合、共振現象により出力信号の強度は入力信号強度の数百倍となる。
（４）共振回路の固有振動数と入力信号の周波数が一致しない場合、共振回路の固有振動数と入力信号の周波数差からうなり現象が発生する。
（５）うなり現象の場合、出力信号の強度は入力信号強度と同程度となる。
（６）共振回路の固有振動数とうなり振動数が一致した場合、出力信号はうなり振動数のみを増幅する。
（７）うなり振動数と共振の場合、出力信号強度は入力信号強度に対して数十分の一に減衰する。
（８）スーパー・ヘテロダイン方式においては、455kHzのうなり現象を発生させ、うなり振動数と共振を利用している。
（９）この場合、出力信号が減衰するため、多段の増幅が必要になると推定される。
（１０）スーパー・ヘテロダイン方式は複雑でコストアップになりそうです。
５章：ゲルマラジオキット Ｃｒｙｓｔａｌ Ｒａｄｉｏ ２ＰＫ２３００に行く。