１章：ニュートン法により代数方程式の解を求める
ニュートン法は任意の関数「y=F(x)」においてy0の値を満足するx0の値を求める方法として極めて有効な数値計算方法である。
１．計算方法の原理
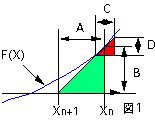
図1において、任意の関数F(X)を青の線で示してある。
任意のXの値Xnと関数F(Xn)の接線とX軸で緑色の三角形ができる。同様に関数F(Xn)の接線とXを微小量変化させてできる赤色の三角形は相似形となる。
相似の法則からA:B=C:Dの関係が成立する。変形すると
A=C×B/D --- (式1)
次のXの値をXn+1を以下の式で求める。
Xn+1=Xn-A --- (式2)
ここで
B=F(Xn) --- (式3)
赤色の三角形のX方向微小変化量を±ΔXとすると
C=2×ΔX --- (式4)
D=F(X+ΔX)−F(X-ΔX) --- (式5)
である。
(式2)に(式1)、(式3)、(式4)、(式5)を代入して、次のXのXn+1を求めることができる。この操作を繰り返すと「F(X)=0」を満足するXの値に収束する。
これをJava Scriptで表現すると
N=10; dX=0.05;
for(i=0;i < N;i++) x=x-FX(x)*2*dX/(FX(x+dX)-FX(x-dX));
となる。ここでdX=ΔXは任意の微小量、Nは繰り返し計算回数である。またFX(x)=F(x)はfunction FX(x){ return y;}として任意の関数を定義する。(プログラムで使える記号の制限で変更)
２．
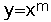の解を求めるサンプルプログラム
以下のフォームに定数を入力して下さい。
トップページに戻る。