2章:数値積分
 積分の定義や意味の理解は容易に理解できますが、実際に任意の関数を与えられて代数的に解を求めようとすると以外と難しい場合があります。代数的に解くのが難しい場合、数値積分を使うのが一番です。数値積分は難しくありません!!しかも、どんな関数でも同じ方法で解を求めることができるので大変便利です。
積分の定義や意味の理解は容易に理解できますが、実際に任意の関数を与えられて代数的に解を求めようとすると以外と難しい場合があります。代数的に解くのが難しい場合、数値積分を使うのが一番です。数値積分は難しくありません!!しかも、どんな関数でも同じ方法で解を求めることができるので大変便利です。
1.数値積分とは?
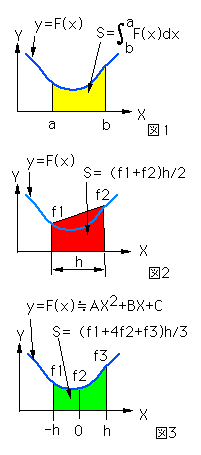
図1において、任意の関数「y=F(x)」とX軸と範囲a〜bで囲まれる面積(黄色の部分)を計算で求めることを数値積分といいます。簡単に言えば面積の計算です。
図2に簡単な面積計算の方法を図2に示します。範囲hとf1とf2で囲まれる台形(赤色の部分)の面積「S」は
S=(f1+f2)h/2 ----(式1)
で求めることができます。任意の関数「y=F(x)」の範囲a〜bを微小範囲hで分割し台形面積の合計を求めれば、図1の黄色の面積を求めることができます。
微小範囲hを十分小さくすれば、(式1)でかなり正確な面積が求まります。(式1)は十分実用的な数値積分の方法のひとつです。
2.より精度の高い数値積分の方法
図3は任意の関数「y=F(x)」の範囲-h〜hで3点の値f1とf2とf3を2次の関数
Y=A(X)^2+BX+C ----(式2)
(ここで^2は2乗の意味で使用しています。)
で近似し、図3の緑色の部分の面積を(式2)から求めると
S=(f1+4f2+f3)h/3 ----(式3)
となります。嘘のように簡単な式になりますが(式2)は容易に代数的積分が可能であり、範囲-h〜hを代入して整理するとこうなります。難しい代数ではないので一度試してみて下さい。
このように高次の累乗の関数で近似することにより計算の精度を高めることができます。より高次の累乗の関数で近似した場合の面積を求める式は以下のようになります。
3次式で近似の場合
S=(f1+3f2+3f3+f4)3h/8 ----(式4)
4次式で近似の場合
S=(7f1+32f2+12f3+32f4+7f5)2h/45 ----(式5)
これ以上もできますが実用的には(式5)までで十分です。
以上の数値積分は「シンプソンの公式」であり累乗の関数近似と等間隔を前提とした計算方法です。これ以外に周期関数を用いたり、不等間隔を用いた方法がありますが複雑になります。計算精度と速度の点でおすすめは(式3)か(式5)です。
3.正規分布の確率を求めるサンプルプログラム
S=(f1+4f2+f3)h/3 ----(式3)を用いました。
確率密度関数が正規分布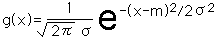
 トップページに戻る。
トップページに戻る。