３章：常微分方程式
電気回路現象や物体の運動等の大部分は常微分方程式のような数学モデルで表現されます。しかし、代数的に解くことが困難な場合が多く、数値計算により解決せざる得ません。数値計算を用いることにより、ほとんどの常微分方程式の解を求めることができるので大変便利です。
１．オイラー法とは？
常微分方程式は一般に以下式であらわされます。
(dy/dx)=f(x,y) ----（式1）
（式1）の意味はxに対するyの変化率が関数f(x,y) で与えられるということです。
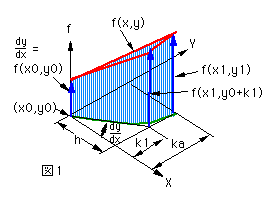
図１において、初期値(x0,y0)における(dy/dx)はf(x0,y0) により与えられます。ここでxをhだけ変化させた場合のyの変化は以下の式で近似的に求めることができます。
k1=hf(x0,y0) ----（式2）
次のxとyの値をそれぞれ以下の式で求めます。
x1=x0+h -----------（式3）
y1=y0+hf(x0,y0) ----（式4）
上記（式3）と（式4）を繰り返し計算することにより、xの値に対するyの値が次々と求まります。この計算を実行するにあたってはxの変化量hは十分小さくする必要があります。また初期値(x0,y0)を与える必要があります。
２．ルンゲ・クッタ法
オイラー法は計算式が単純ですが、xの変化量hの間でxとyの関係が直線で近似できるという条件が必要です。ルンゲ・クッタ法は巧妙なテクニックで計算の精度を上げています。
２次のルンゲ・クッタ法は以下のようになります。
k1=hf(x0,y0) ---------（式5）
k2=hf(x0+h,y0+k1) ----（式6）
ka=(k1+k2)/2 ---------（式7）
次のxとyの値をそれぞれ以下の式で求めます。
x1=x0+h -----------（式8）
y1=y0+ka ----------（式9）
これはyの変化量kaをf(x0,y0)とf(x0+h,y0+k1)の平均値から求めているわけです。これによりxとyの関係が２次の場合まで正確に近似しています。（数学的証明はくどいので省略させていただきます。）
４次のルンゲ・クッタ法は以下のようになります。
k1=hf(x0,y0) -------------（式10）
k2=hf(x0+h/2,y0+k1/2) ----（式11）
k3=hf(x0+h/2,y0+k2/2) ----（式12）
k4=hf(x0+h,y0+k3) --------（式13）
ka=(k1+2k2+2k3+k4)/6 ----（式14）
次のxとyの値をそれぞれ以下の式で求めます。
x1=x0+h -----------（式15）
y1=y0+ka ----------（式16）
常微分方程式の数値計算法としては上記４次のルンゲ・クッタ法を用いるのが一般的です。ちなみにf(x,y)がyに無関係で(dy/dx)=f(x)としてあらわされる場合、「ka=(f(x0)+4f(x0+h/2)+f(x0+h))h/6」となってシンプソンの積分公式と一致します。
３．連立ルンゲ・クッタ法
一般の常微分方程式は高階常微分方程式となったり、連立の常微分方程式となることが数多くあります。若干計算方法は繁雑となりますが連立ルンゲ・クッタ法でこれらの解を求めることができます。
2階常微分方程式は一般に下記の（式17）で表わされます。
y''=f(x,y,y') ----------（式17）
dy/dx=Z ----------（式18）
とすれば（式17）は
dz/dx=f(x,y,z) --------（式19）
となり、（式18）と（式19）の連立常微分方程式として表わすことができます。従って高階常微分方程式と連立の常微分方程式は同じ方法で解くことができます。
一例として、2元連立常微分方程式の解き方を以下に示します。
dy/dx=f(x,y,z) --------（式20）
dz/dx=g(x,y,z) --------（式21）
において、
K1=hf(x0,y0,z0) -------------（式22）
L1=hg(x0,y0,z0) -------------（式23）
K2=hf(x0+h/2,y0+K1/2,z0+L1/2) ----（式24）
L2=hg(x0+h/2,y0+K1/2,z0+L1/2) ----（式24）
K3=hf(x0+h/2,y0+K2/2,z0+L2/2) ----（式25）
L3=hg(x0+h/2,y0+K2/2,z0+L2/2) ----（式26）
K4=hf(x0+h,y0+K3,z0+L3) --------（式27）
L4=hg(x0+h,y0+K3,z0+L3) --------（式28）
Ka=(K1+2K2+2K3+K4)/6 ----（式29）
La=(L1+2L2+2L3+L4)/6 ----（式30）
次のxとyとzの値をそれぞれ以下の式で求めます。
x1=x0+h -----------（式31）
y1=y0+Ka ----------（式32）
z1=z0+La ----------（式33）
ちょっと複雑ですが（式22）〜（式33）を使って解くことができます。3元、4元についても同じ考え方で拡張できます。そもそも微分方程式とは複雑でわかりにくいものです。式の数の多さはありますが一つ一つの式は単純計算ですのでめげないでトライしましょう。
４．CR回路の出力信号を求めるサンプルプログラム
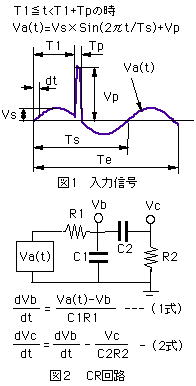図１に示す入力信号を図２に示すCR回路に通した場合の出力信号を求めます。
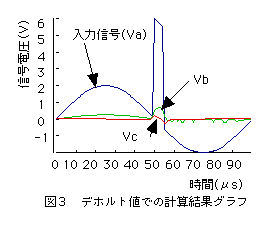
５．CR回路のデホルトサンプル計算結果グラフ
CR回路のデホルトサンプル計算結果グラフを以下に示します。これからこの回路は信号を減衰させる働きがあることがわかります。
トップページに戻る。