５章：光学の基礎
カメラは記念写真用のみでなく、さまざまな工学分野で応用されています。カメラには必ずレンズがついています。レンズで光の像をフィルム等の感光材料に結像するか、もしくはCCDイメージセンサに結像し電気信号に変換しています。
レンズは必ずしも正確に原画を投影できる訳ではありません。どんな小さなパターンでも投影できる訳ではありません。レンズには必ず設計製作上の誤差（専門的には収差と言います。）があり投影像は劣化します。収差の小さい高性能レンズに関しての日本の技術は世界随一と言っても過言ではないでしょう。しかし、ここで収差について論ずるつもりはありません、収差については専門メーカにおまかせしましょう。
今、仮りに収差ゼロの無収差レンズができたとしましょう、それでも投影像は劣化します。なぜでしょうか？これは光が波動の性質をもっており、直進せずに広がってしまうからです。
１．光の波動とは？
光を別の表現をすると電磁波の一種であり、電場と磁場の周期的変化と言われています。これを式で表わすと、
U(x,t)=A(x)・(cos(β(x)+ωt)+i・sin(β(x)+ωt)) ---（式1）
ここでxは距離であり、tは時間である。光の波動は距離(x)と時間(t)の周期関数と表わされ、複素関数となっています。何とも理解しがたいがしかたない！！
波動の絶対値A(x)は光源からの距離(x)に反比例し、A(x)=A/xの関係があります。しかし、今後議論を簡単にするため、時間項とA(x)項を無視します。
U(x)=(cos(β(x))+i・sin(β(x))) ---（式2）
または
U(x)=EXP(i・β(x)) ---（式3）
として扱います。（式2）と（式3）は全く同じです。
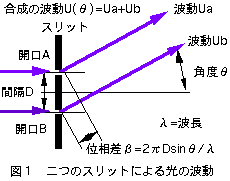
図１に二つのスリットによる光の波動の合成の例を示します。図１において開口Aを通過した光の波動の位相を基準にするとβa=0となり、
Ua=1 ---（式4）
開口Bを通過した光の波動の位相はβb=-2πDsinθ/λとなり、
Ub=EXP(-i2πDsinθ/λ) ---（式5）
光の波動の合成は
U(θ)=Ua+Ub=1+EXP(-i2πDsinθ/λ) ---（式6）
となります。（式6）は光の波動の合成が単純に絶対値の和ではなく、方向をもったベクトル和として表現されています。（式6）の波動の絶対値は0〜2の間で変化します。
また、光の強度は波動の絶対値の自乗として求めることができます。従って（式6）の光の強度は0〜4の間で変化します。
ベクトルの方向と光の波動の位相(β)は同じ意味です。β=-2πDsinθ/λであり、間隔(D)と角度(θ)と波長(λ)で光の波動と強度が決まります。
２．幅のあるスリットの光の波動の合成方法
上記（式6）においてはスリットの幅を無限小と仮定していますが、実際には幅を考慮する必要があります。今、有限幅の微小範囲(Δx)での光の波動を以下のように表わします。
ΔU(θ)=EXP(-i2πsinθ・x/λ)(Δx/λ) ---（式7）
（式5）と（式7）ではDのかわりにx、そして無次元数(Δx/λ)がかけてあります。Δxをかけないと連続的な扱いができません。波長(λ)で割っているのは無次元数にするためです。
スリットの幅をx1からx2とした場合、幅のあるスリットの光の波動は（式7）の総和として求まります。
U(θ)=Σ(EXP(-i2πsinθ・x/λ)(Δx/λ)) ---（式8）
（式8）において総和の範囲はx1からx2までです。Δxを無限小にした場合、（式8）は連続的な定積分の式となります。（式8）はこのまま数値積分を実行して解を求めることができますが代数的に解くことができます。代数解は以下のようになります。
K=2π/λ ---（式9）とします。
（１）実数部
θ=0の場合
Ur(θ)=(x2-x1)/λ ---（式10）
θ=0以外の場合
Ur(θ)=(sin(-Ksin(θ)x1)-sin(-Ksin(θ)x2))/(2πsin(θ)) ---（式11）
（２）虚数部
θ=0の場合
Ui(θ)=0 ---（式12）
θ=0以外の場合
Ui(θ)=(cos(-Ksin(θ)x2)-cos(-Ksin(θ)x1))/(2πsin(θ)) ---（式13）
（式9）〜（式13）では実数部と虚数部を別々に計算します。（C言語等では直接複素数の計算をサポートしていますがJava Scriptでは直接複素数の計算はできません。）
３．レンズとは？
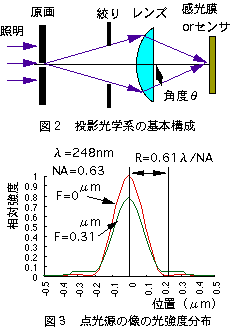
図２の投影光学系の基本構成を示します。
投影光学系で最も重要な要素は照明の光の波長(λ)とレンズを通して結像する光の角度(θ)です。
光の角度は開口数(Numerical Aperture)NAとして以下の式で定義されます。
NA=sinθ ---（式14）
また、カメラのレンズ絞りではFナンバーが用いられています。
F=1/(2sinθ) ---（式15）
光の波長(λ)と開口数(NA)が決まると、一般的に解像度(R)は、
R=0.61λ/NA ---（式16）
焦点深度(D)は、
D=±0.5λ/(NA^2) ---（式17）
として簡易的に計算できます。ここで^2は自乗の意味です。
カメラで撮影の経験がある方はおかしい？「晴れた日にレンズ絞りを絞ってFナンバーを大きくして撮影した方が解像度が良く、奇麗に写る。」そんな経験が多いと思いますが（式16）と（式17）はレンズの収差を考慮していません。収差が極端に少ない場合のみですので一般的なカメラにはあてはまりません。
さらには、（式16）と（式17）は理想点光源を投影した場合の式であり、R=0.61λ/NAは理想点光源の光の広がりの半径を示しているだけです。
波長λ=248nm、NA=0.63での点光源像の光強度分布を図３に示します。
この場合、R=0.24μm、D=±0.31μmとなり、フォーカス値F=0.31μmでは、相対的に光強度が80%程度に劣下します。
（式16）と（式17）は決して厳密な式ではありません。しかし、0.24μm以下のパターンを投影することは理論的にも容易でないことを暗示しているのです。
４．パターンの投影像の光強度分布を求めるには？
任意のパターンの投影像の光強度分布を図３に示すように求めるには光の広がりを２次元的に計算する必要があり、かなりの計算量となります。レンズは丸いため２次元でないと正しくありませんが「Java Script」の処理速度では無理がありそうです。ここでは、１次元で計算してみたいと思います。
図２の絞りの位置を「瞳」と呼びます。瞳面での光の波動は前述の
U(θ)=Σ(EXP(-i2πsinθ・x/λ)(Δx/λ)) ---（式8）
で与えられます。この光の波動は球面状に広がっていきますがレンズを通過すると一点（焦点）に収束する逆向きの球面状の波動に変換されます。
像面での位置を（x）、焦点誤差を（F）とした場合、像面での光の波動V(x)は以下の式で計算できます。
V(x)=Σ(U(θ)・EXP(iβ)・Δθ) ---（式18）
β=K(x・sinθ+F・cosθ) ---（式19）
K=2π/λ ---（式9）
ここで（式18）のΔθを無限小とした場合、（式18）は定積分の式となります。
定積分の範囲は
θ1=-asin(NA) から θ2=asin(NA)
となります。
（式18）は図２の原画に垂直に照明した場合の像面での光の波動を与えます。像面での光の強度は光の波動の絶対値の自乗、すなわち実数部の自乗と虚数部の自乗の和として求めることができます。
実際の照明においては平行光であることは稀であり、角度を持っています。角度を持った照明光は互いに干渉しませんので像面での光の強度の合成で照明光の角度の影響を計算します。
この照明光の角度の影響は照明σであらわされます。照明光の角度θは
θ=σ・asin(NA) ---（式20）
の関係があります。なお照明光の角度がθの場合、瞳面での光の波動U(θ)はθだけオフセットを持ちます。
以上の計算式は一次元の式であり二次元ではありませんのでレンズの円形の影響を考慮していません。正確には二次元にする必要がありますが考え方は同じです。
５．像面での光の強度計算サンプルプログラム
６．サンプルプログラム計算結果例
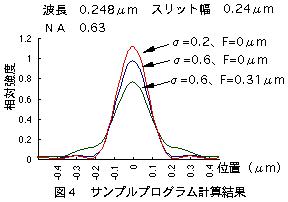図４にサンプルプログラム計算結果例を示します。
（１）フォーカスがベストからずれると俗にいう「ピンボケ」となり画質が劣下する。これは当然の結果ですが実用的には深刻な問題です。感光材料は薄膜としてコーティングしますがその厚さは0.3μmよりも厚いのです。これでは感光材料の厚さだけで「ピンボケ」となってしまいます。
（２）孤立のスリットでは照明条件がハイコヒーレント（σ=0.2）の方が一般的な照明条件（σ=0.6）よりもコントラストが良くなりますがこれは一般的なパターンでは成立しません。（単純なラインとスペースの繰り返しパターンではσが大きい方がよくなります。）
（３）サンプルプログラムは処理時間の制約からかなり手抜きとなっております。（複雑なパターンは計算できませんし、近似解です。）
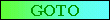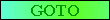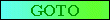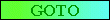トップページに戻る。