６章：画像信号処理方法
カメラの画像信号用いて自動位置合わせを行う方法は比較的に多く行われています。その多くでテンプレートマッチングと呼ばれる画像信号処理方法が用いられています。画像信号処理による自動位置合わせでは画像信号のS/N起因のトラブルがよく発生することがありますので画像信号処理の原理を理解し対処することが必要となる場合があります。
１．テンプレートマッチングの原理
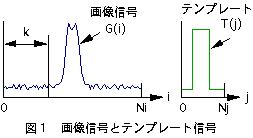
テンプレートマッチングは図１に示すような画像信号(G(i))とテンプレート(T(j))の一致度を計算し、一致度の最も良い位置を求めるのを基本原理としています。
図１において、iは画像信号の絵素、jはテンプレートの絵素、kは一致度の計算位置を示しています。
ここでiは
i=k+j ----式（1）
の関係があると定義します。
iがマイナスあるいはNi以上となるのはまずいのでkの変化範囲は
0≦ k ≦ Ni-Nj ----式（2）
とします。
計算位置(k)での一致度(M(k))を以下のように定義します。
M(k)=Σ(G(i)-T(j))^2 ----式（3）
^2は自乗に意味で使用しています。
総和の範囲はj=0〜j=Njとします。
式（3）は一致度(M(k))を画像信号とテンプレートの差分の総和として定義しています。この計算を実行するとkがテンプレートの形状と一致した位置でM(k)が最小となります。M(k)の最小値を求めることによりパターンの位置を求めることができます。
式（3）は単純ですが実用上は優れた方法とは言えません。なぜなら一般に画像信号の暗レベルや信号の高さは検出した対象により変化するため一致度が悪くなります。このような問題を解決する方法としては平均値や標準偏差を用いて信号を正規化する方法があります。正規化することにより信号の暗レベルや信号の高さに影響されずに単に形状の一致度のみを計算できます。
正規化した画像信号Gs(i)は以下となります。
Gs(i)=(G(i)-Ag)/σg ----式（4）
Ag=G(i)の平均値（範囲はj=0〜j=Nj）
σg=G(i)の標準偏差（範囲はj=0〜j=Nj）
同様に正規化したテンプテートTs(i)は以下となります。
Ts(j)=(T(j)-At)/σt ----式（5）
At=T(j)の平均値（範囲はj=0〜j=Nj）
σt=T(j)の標準偏差（範囲はj=0〜j=Nj）
正規化した画像信号Gs(i)とテンプテートTs(i)を用いて一致度(M(k))を以下のように定義します。
M(k)=(Σ(Gs(i)-Ts(j))^2)/N ----式（6）
^2は自乗に意味で使用しています。
ここでNはデータの個数でN=Nj+1となります。
式（5）を変形すると
M(k)=2・(1-(Σ(Gs(i)・Ts(j)))/N) ----式（7）
となり0〜4の間の値をとりうることがわかります。
一致度(M(k))は以下のようにも定義できます。
M(k)=(Σ(Gs(i)・Ts(j)))/N ----式（8）
式（5）は差分の自乗和であり、式（7）は相関度を求める式ですが式を展開してみると本質的には同一の結果が得られることがわかります。
式（7）の値は-1〜1の間で変化し、一致度の最も良い位置で最大となります。式（7）が最も一般的なパターンマッチング方法として広く利用されていますが差分の自乗和でも同じ結果となります。
式（7）をさらに展開すると以下のようになります。
M(k)=(N・Σ(G(i)・T(j))-(ΣG(i))・(ΣT(j)))/(N・σg・N・σt) ----式（9）
N・σg=sqrt(N・Σ(G(i)^2)-(ΣG(i))^2) ----式（10）
N・σt=sqrt(N・Σ(T(j)^2)-(ΣT(j))^2) ----式（11）
ここでsqrtは平方根、Nはデータ数、総和範囲はj=0〜j=Njです。
上記の総和範囲は一次元で定義しましたが二次元でも全く同じ式となります。
実用的には二次元的な計算が必要であり、大量のデータを高速で計算する必要があるため、専用のハード演算回路を用いるのが一般的です。
２．対称性パターンマッチングの原理
前述のテンプレートマッチングはテンプレートが必要ですが対称性パターンマッチングではテンプレートを使用しません。かわりに対称性の一致度を計算し、一致度の最も良い位置を求めるのを基本原理としています。
iは画像信号の絵素、jは対称性演算範囲の変数（jの範囲は±Nj/2）、kは一致度の計算位置とします。
iがマイナスあるいはNi以上となるのはまずいのでkの変化範囲は
Nj/2 ≦ k ≦ Ni-Nj/2 ----式（12）
とします。
計算位置(k)での一致度(M(k))を以下のように定義します。
M(k)=Σ(G(k+j)-G(k-j))^2 ----式（13）
^2は自乗に意味で使用しています。
総和の範囲はj=-Nj/2〜j=Nj/2とします。
式（13）は一致度(M(k))を画像信号の左右の差分総和として定義しています。この計算を実行するとkが対称性の良い位置でM(k)が最小となります。M(k)の最小値を求めることによりパターンの位置を求めることができます。
式（13）においても正規化するのはより良い改善です。また、差分の自乗和と相関度は本質的に同じであることを考慮すると
M(k)=(Σ(Gs(k+j)・Gs(k-j))/N ----式（14）
Gs(k+j)=(G(k+j)-Ag)/σg ----式（15）
Ag=G(k+j)の平均値（範囲はj=-Nj/2〜j=Nj/2）
σg=G(k+j)の標準偏差（範囲はj=-Nj/2〜j=Nj/2）
と対称性の一致度を定義できます。式（14）の値は-1〜1の間で変化し対称性の良い位置で最大となります。
式（14）をさらに展開し、整理すると以下のようになります。
M(k)=(N・Σ(G(k+j)・G(k-j))-(ΣG)^2)/(N・Σ(G^2)-(ΣG)^2) ----式（16）
なお、総和の範囲j=-Nj/2〜j=Nj/2において「ΣG=ΣG(k+j)=ΣG(k-j)」の関係があります。（N=Nj+1の関係もあります。）
テンプレートマッチングと対称性パターンマッチングはそれぞれ一長一短があり、いちがいにどちらが優れているとはいえません。認識の安定性ではテンプレートマッチング、精度で対称性パターンマッチングではないかと思っています。用途による使い分けがベストでしょう。ただし、商業目的への適用については問題が生じることがあります。
３・画像信号処理サンプルプログラム
３．サンプルプログラム計算結果
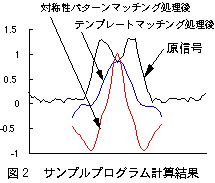
図２にサンルププログラムのデホルト値での計算結果を示します。
図２において原信号はかなり複雑な波形となっており、このままでは波形の中心位置を正確に求めるのは難しいものがあります。
この原信号に対し、テンプレートマッチング処理をほどこすとかなり処理しやすい波形に変換されていることがわかります。単純に最大位置が波形の中心として求めることができます。最大位置の算出は最小自乗2次曲線近似を用いるのが一般的です。最小自乗2次曲線近似の方法は一般によく知られており、ここでは省略します。
原信号に対し、対称性パターンマッチング処理をほどこすと波形はシャープとなり、さらに処理しやすい波形に変換されていることがわかります。
サンプル条件では対称性パターンマッチング処理がベストとなっていますが、それぞれ一長一短があることを忘れてはいけません。実際の画像信号をとり、さまざまな処理条件で比較評価することが重要です。
トップページに戻る。