7章:Gauss-Newton法
Gaussの名の付く数学は一般的に難解ですね!!数値計算法としてこれ以外に「ガウス求積」という方法があります。計算精度は良いのですが難解です。
Gauss-Newton法と同じことを第1章のニュートン法でも行うことができます。しかし、Gauss-Newton法はすこし難解です。
一般に多数の測定データを関数近似する場合、最小自乗法が用いられます。関数が直線やN次累乗関数の場合は代数的に関数のパラメータを求めることができます。
このような場合、数値計算法を使う必要はありません。代数解は最も高速で正確に計算できます。
しかし、いつも代数的に解が求まるとは限りません。例えば膜厚測定機の例を考えてみましょう。反射率は光の波長、入射角度、偏光角度、屈折率、光吸収係数、膜厚の関数として求めることができます。
波長、入射角度、偏光角度あらかじめわかっており、反射率は測定により求めることができます。波長、入射角度、偏光角度と反射率から屈折率、光吸収係数、膜厚を求める訳ですが代数的に求めることはできません。
光の波長、入射角度、偏光角度、屈折率、光吸収係数、膜厚から反射率を求め、最も反射率のカーブが一致する屈折率、光吸収係数、膜厚をさがすのです。
反射率の計算式はかなり複雑で最小自乗法を用いても代数解は求まりません。第1章のニュートン法でもよいのですが計算速度と精度の点でGauss-Newton法は優れた方法です。
1.Gauss-Newton法とは?
説明を簡単にするため、未知のパラメータは(a,b)の2個とします。
関数は
Y=f(X,a,b) ----(1式)
とします。(反射率をY、入射角度をXと考えてもよいでしょう。)
入射角度Xは自由に変えることができますのでXiとします。Xiに対応したYiは測定データとして得たとします。
ここで誤差関数E(a,b)を以下の様に定義します。
Si(a,b)=f(Xi,a,b)-Yi ----(2式)
E(a,b)=Σ(Si(a,b))^2 ----(3式)
(^2は自乗の意味です。)
ここで、パラメータa,bをそれぞれΔa,Δbだけ変化させると(3式)は
E(a+Δa,b+Δb)=Σ(Si(a+Δa,b+Δb))^2 ----(4式)
となります。誤差が最小となる条件においては、(4式)をaとbで偏微分した式が零となる必要があります。
aとbを任意の初期値として与えると未知数はΔa,Δbであり、式は2個ですからΔa,Δbの値は決定されます。
次の値はa=a+Δa、b=b+Δbとして繰り返し計算すると誤差が最小となるようにa,bの値が収束します。
以上がGauss-Newton法の基本原理です。
具体的に(4式)を偏微分すると以下のようになります。
Si(a,b)をaで偏微分したものを(Sia)とします。
Si(a,b)をbで偏微分したものを(Sib)とします。
Σ{Si(Sia)+Δa(Sia)(Sia)+Δb(Sia)(Sib)}=0 ----(5式)
Σ{Si(Sib)+Δa(Sia)(Sib)+Δb(Sib)(Sib)}=0 ----(6式)
なお、微小項を全て無視して
Si(a+Δa,b+Δb)≒Si(a,b)+Δa(Sia)+Δb(Sib) ----(7式)
(Si(a,b)+Δa(Sia)+Δb(Sib))^2≒Si(a,b)^2+2ΔaSi(a,b)(Sia)+2ΔbSi(a,b)(Sib) ----(8式)
(^2は自乗の意味です。)
の関係を利用しています。
また、(Sia)、(Sib)の高次偏微分項は無視しています。(荒っぽいですが。)
(5式)(6式)から
Daa=Σ{(Sia)(Sia)}----(9式)
Dab=Σ{(Sia)(Sib)}----(10式)
Dbb=Σ{(Sib)(Sib)}----(11式)
Dia=Σ{Si(a,b)(Sia)}----(12式)
Dib=Σ{Si(a,b)(Sib)}----(13式)
Δa=(Dib*Dab-Dia*Dbb)/(Daa*Dbb-Dab*Dab)----(14式)
Δb=(Dia*Dab-Dib*Daa)/(Daa*Dbb-Dab*Dab)----(15式)
となります。
2.Gauss-Newton法サンプルプログラム
膜厚を求める計算は複雑なのでかわりに以下の関数とします。
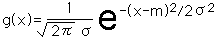
ここでY=g(X)、X=h*i、m=a、σ=bとします。
hはXの刻み幅です。
 トップページに戻る。
トップページに戻る。