プログラム：XYテーブルの応答特性

　XYテーブル
　XYテーブルはほとんどの装置で必要となる基本的な機構です。しかし、ステージに要求される仕様はさまざまであり、多様な方式のXYテーブルが必要となります。
　XYテーブルは駆動機構とガイド機構から構成されますが、さまざまな方式があります。　高速・高精度のXYテーブルの駆動機構としては、従来ボールネジ方式が数多く採用されていましたが、近年の主流はリニアーモータ方式となっています。これはリニアーモータ方式が高速・高精度を実現しやすいためです。
　プログラムBでは、ボールネジ方式とリニアーモータ方式のXYテーブルの応答特性が計算できます。ボールネジ方式とリニアーモータ方式の応答特性の差については、種々のパラメータを設定し、応答特性の違いを計算することにより、特性の差が明らかになるでしょう。

　ボールネジ方式XYテーブル
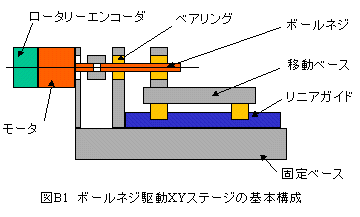
　図B1にボールネジ方式XYテーブルの基本構成を示します。応答特性を計算するためには、単純な数式で表現できるようにモデル化が必要です。厳密に考えると式は複雑になり、計算が難しくなります。逆に単純すぎると実際の現象が計算結果に現れなくなります。
　モデル化にあたって重要なポイントは図B1におけるボールネジとナットの剛性、ベアリングの剛性、ナットと移動ステージの結合部品の剛性、ベアリングを支持する部品の合成等ですが、計算モデルではこれらを一まとめにして単純にバネ定数(K)として表現します。
　このバネ定数(K)が大きければXYテーブルの応答特性は改善しますが、実際の値でバネ定数(K)を大きくするのは難しく限界があります。
　

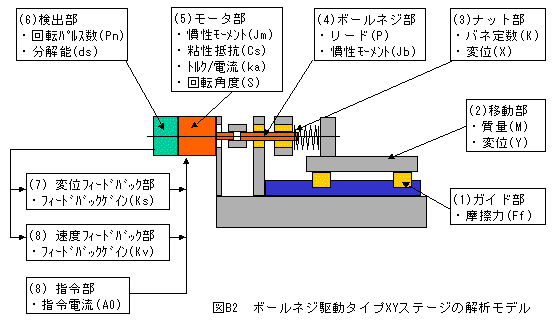
　ボールネジ駆動タイプXYステージの解析モデルの方程式　　図B2に示すモデルを数学的な方程式で表現すると下記式となります。

上記の(1)式は回転→直線変換式であり、説明するまでもありません。
(2)式は移動部の運動方程式です。ここで±Ffの項は摩擦力の項であり、扱いに注意が必要です。摩擦力は運動の速度を落とす方向に働きます。速度の正負によって摩擦力の正負が切り替わる不連続な関数です。
(3)式はモータの運動方程式です。ここでモータには変位と速度に比例した電流がフィードバックされます。（線形フィードバック制御）注意しなければならない点は変位(ds*Ps)と速度(ds*dPs/dt)はデジタルであり不連続に変化することです。
(4)式はﾊﾟﾙｽ数(Pn)を与えるデジタル化の式です。

　特性パラメータの推定と単位の統一化
　前記の方程式を解くためには、単位が統一された特性パラメータの値を設定する必要があります。この作業は以外と厄介な作業で正確な値が不明な場合は、推定値を用います。また、慣用的に用いられる単位は統一されていませんので単位の変換が必要です。
　表１に変換前の特性パラメータの推定値例を示します。
表１　変換前の特性パラメータの推定値例

No	特性仕様	記号	値	単位	備考
1	モータの慣性モーメント	Jmo	0.12	gfcms^2	カタログデータ
2	ボールネジ半径	BSr	6	mm	図面データ
3	ボールネジ長さ	BSL	650	mm	図面データ
4	鉄の比重	Feρ	0.0000079	kg/mm^3	物理表
5	ボールネジリード	P	4	mm	図面データ
6	モータトルク	Mt	0.319	N・m	カタログデータ
7	最大回転数	N	4000	rpm	カタログデータ
8	モータ定格電流	MI	1.3	A	カタログデータ
9	ﾛｰﾀﾘｴﾝｺｰﾀﾞ分割数	RE	4000	分割	カタログデータ
10	移動質量	M	60	kg	推定値
11	摩擦抵抗	Ffo	0.5	kgf	推定値
12	バネ定数	Ko	1	kgf/um	推定値

　表１の特性パラメータの内1～9はカタログ、図面等から値を知ることができます。移動質量、摩擦抵抗、バネ定数は実物があれば実測可能です。この３つのパラメータはXYテーブルの応答特性を大きく左右しますが、組立て、出荷検査できちんと管理されてないのが現状です。とりあえず推定値を用います。
　表１から換算できないパラメータとしては、変位フィードバックゲインと速度フィードバックゲインがあります。これについては、シミュレーション結果をみて調整します。
　換算後の特性パラメータを表2に示します。
　表２　換算後の特性パラメータ例

No	特性仕様	記号	値	単位	計算式	備考
1	モータの慣性モーメント	Jm	11.76	Kg*mm^2	Jm=Jmo98010*10/1000	単位変換
2	ボールネジ慣性モーメント	Jb	10.453	Kg*mm^2	Jb=πBSr^4BSL*Feρ/2	ﾓｰﾒﾝﾄ計算
3	ボールネジリード	P	4	mm	－	－
4	粘性抵抗	Cs	761.556	Kg*mm^2/s	Cs=10^6Mt/(2π*N/60)	ﾄﾙｸと回転数
5	電流換算トルク	Ka	245384.615	Kgmm^2/(s^2A)	Ka=10^6*Mt/MI	ﾄﾙｸ/電流
6	角度検出分解能	ds	0.00157	rad	da=2*π/RE	単位変換
7	移動質量	M	60	kg	－	－
8	摩擦抵抗	Ff	4900	kg*mm/s^2	Ff=Ffo*9800	単位変換
9	バネ定数	K	9800000	Kg/s^2	K=98001000Ko	単位変換

　リニアーエンコーダ使用の場合の計算式
　以上のXYステージ計算モデルは、検出器としてはロータリーエンコーダを前提に議論してきましたが、XYステージの検出器としてはリニアーエンコーダやレーザ測長機が用いられることがあります。
　この場合回転検出から直線検出に変換するする必要がありますが、計算式の変更箇所は僅かです。
　リニアーエンコーダやレーザ測長機の最小分解能を(dx)とします。

　計算の実行
　VBAソフト「ｽﾃｰｼﾞ1.xls」をダブルクリックして起動した後、シート「デェフォルト条件」の条件表の内容をシート「IN_FM」にコピーします。
次にシート「操作」の「計算実行」ボタンを押します。
計算結果の概要が表示されます。

デフォルト条件表　


No	記号	値	単位	説明
1	Et	0	整数	ロータリエンコーダの場合Et=0、リニアエンコーダの場合Et=1を設定する。
2	ds	0.00157	rad	ロータリエンコーダ角度検出分解能、単位(rad)(ロータリエンコーダ指定時有効）
3	dx	0.00005	mm	リニアエンコーダ検出分解能、単位(mm)(リニアエンコーダ指定時有効）
4	Jm	11.76	Kg*mm^2	モータの慣性モーメント、単位(Kg*mm^2)
5	Jb	10.45	Kg*mm^2	ボールネジ慣性モーメント、単位(Kg*mm^2)
6	P	4	mm	ボールネジリード、単位(mm)
7	Cs	761.55	Kg*mm^2/s	モータ粘性抵抗、単位(Kg*mm^2/s)
8	Ka	245384.6	Kgmm^2/(s^2A)	電流あたりのモータトルク,単位(Kgmm^2/(s^2A))
9	M	60	kg	移動部質量、単位(kg)
10	Ff	4900	kg*mm/s^2	摩擦抵抗、単位(kg*mm/s^2)
11	K	9800000	Kg/s^2	バネ定数、単位(Kg/s^2)
12	Ks	10	A/mm	変位フィードバックゲイン、単位(A/mm)
13	Kv	0	A*s/mm	速度フィードバックゲイン、単位(A*s/mm)
14	A0	0	A	指令電流（目標設定）、単位(A)
15	Y0	0.01	mm	ナット部変位初期値、単位(mm)
16	Y1	0	mm/s	ナット部速度初期値、単位(mm/s)
17	Y[2]	0.01	mm	移動部変位初期値、単位(mm)
18	Y[3]	0	mm/s	移動部速度初期値、単位(mm/s)
19	h	0.00001	s	計算時間間隔、単位(s)（計算時間が長くなりますが小さくしたほうが精度がよい。）
20	N	20000	整数	計算回数（整数）（計算時間間隔×計算回数でトータル時間）
21	Np	100	整数	計算結果の出力間隔回数（整数）（計算結果を全て出力すると見苦しくなるため間引きをします。）
22	Ff	4900	kg*mm/s^2	摩擦抵抗
23	K	9800000	Kg/s^2	バネ定数

　デフォルト条件計算結果
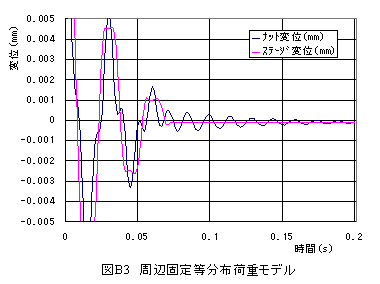
　デフォルト条件計算結果を図B3に示します。
　図B3からナット部分は収束後微小振動が残りますがステージ変位は0.1μm程度オフセットした位置で安定状態となります。
　振動の制定とオフセットに関しては摩擦力が重要な役割を果たしします。振動をきらうか？オフセットをきらうか？によって最適な摩擦力は異なってきます。摩擦力は必ずしも小さければよいと言う訳ではありません。摩擦力がゼロの場合、速度フィードバックを行なわないと振動が収まらなくなります。また±数ビットの微小振動が残ります。

　リニアーエンコーダ使用の場合
　計算条件入力ダイアログでEt=1を設定するとリニアーエンコーダ使用の場合の応答特性を計算します。レーザ測長器を使用の場合も同様で、この場合検出分解能 dxを細かく設定します。

　本計算は単純なモデル計算ですので、バネ定数Kを限りなく大きく設定すれば、応答特性はいくらでも改善できるでしょう。
　しかし、大きなバネ定数が実際に実現できるか？ということは別問題です。
　実際には、回転運動を直線運動に変換し、移動ステージ連結する過程で多くの機構部品を必要とします。
　機構部品は鉄等の弾性材料であるため弾性変形します。従ってバネ定数Kを限りなく大きくすることは困難となります。
　
　リニアーモータは直線運動を直接移動ステージに伝達できるため、応答特性は大幅に改善することが可能です。

リニアーモータXYテーブルの応答特性に行く。

トップページに戻る。