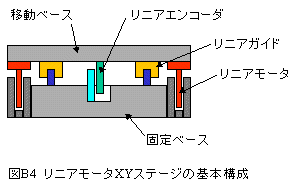
リニアーモータXYテーブルの応答特性


  1. 　リニアーモータXYテーブル
    　リニアーモータXYテーブルの基本構成を図B4に示します。
    　リニアーモータは基本的に磁石とコイルで構成されます。固定マグネット型、 固定コイル型や磁石の配置のしかた等若干のバリエーションがありますが、図B4は 固定マグネット型の例でマグネットが固定ベースに固定されており、コイルが移動ベース に固定されています。
    　コイルに電流を流すと電流に比例した推力が移動ベースに直接伝達されます。
    　移動ベースの位置はリニアエンコーダで直接計測されます。
    　リニアーモータXYテーブルは図B4からわかるように非常にシンプルな構造と なります。このシンプルさが応答性能向上のポイントです。
  2. 　リニアーモータXYステージの解析モデル
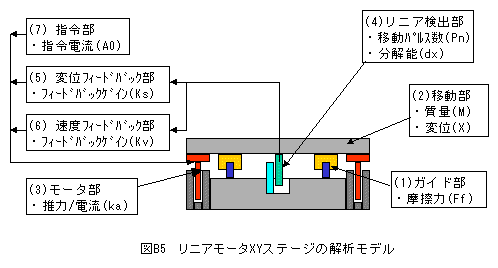
    　リニアーモータXYステージの解析モデルを図B5に示します。
    （１）ガイド部
    ・ガイド部では摩擦力は発生します。これを記号(Ff)単位(kg*mm/s^2)とします。
    （２）移動部
    ・移動部では質量が主要パラメータです。これを記号(M)単位(kg)とします。
    ・移動部は変位を生じます。これを記号(X)単位(mm)とします。
    （３）モータ部
    ・電流あたりのトルクが主要パラメータです。これを記号(Ka)単位(Kg*mm/(s^2*A))とします。
    ・モータの質量と自己発電作用による粘性抵抗は無視します。
    （４）リニア検出部
    ・検出部では変位パルス数を検出します。これを記号(Pn)単位(ﾊﾟﾙｽ)とします。
    ・１パルス当りの変位を分解能とします。これを記号(dx)単位(mm/ﾊﾟﾙｽ)とします。
    （５）変位ﾌｨｰﾄﾞﾊﾞｯｸ部
    ・検出部で検出された変位に一定数をかけてﾌｨｰﾄﾞﾊﾞｯｸします。このｹﾞｲﾝを記号(Ks)単位(A/mm) とします。
    （６）速度ﾌｨｰﾄﾞﾊﾞｯｸ部
    ・検出部で検出された速度に一定数をかけてﾌｨｰﾄﾞﾊﾞｯｸします。このｹﾞｲﾝを記号(Kv)単位(A*s/mm)とします。
    （７）指令部
    ・目標に応じて指令電流を設定します。これを記号(A0)単位(A)とします。
    　
  3. 　リニアモータXYステージの解析モデルの方程式　 　図B5に示すモデルを数学的な方程式で表現すると下記式となります。

    　(1)式の左辺は移動部の運動方程式です。ここで±Ffの項は摩擦力の項であり、扱いに注意が必要です。摩擦力は運動の速度を落とす方向に働きます。速度の正負によって摩擦力の正負が切り替わる不連続な関数です。
    　(1)式の右辺は制御の式です。ここでモータには変位と速度に比例した電流がフィードバックされます。（線形フィードバック制御）注意しなければならない点は変位(dx*Pn)と速度(dx*dPn/dt)はデジタルであり不連続に変化することです。
    　(2)式はﾊﾟﾙｽ数(Pn)を与えるデジタル化の式です。　

  4. 　特性パラメータの推定と単位の統一化
    　前記の方程式を解くためには、単位が統一された特性パラメータの値を設定する必要があります。正確な値が不明な場合は、推定値を用います。また、慣用的に用いられる単位は統一されていませんので単位の変換が必要です。表１に変換前の特性パラメータの推定値例を示します。
    表１　変換前の特性パラメータの推定値例
    No特性仕様記号値単位備考
    1最大推力Pmax864N仕様書
    2最大電流Imax36A仕様書
    3移動質量M40kg仕様書(移動ﾃｰﾌﾞﾙ+積載）
    4摩擦抵抗Ffo8N推定値
    5分解能dx0.00005mm仕様書
    　

    　表１から換算できないパラメータとしては、変位フィードバックゲインと速度フィードバックゲインがあります。これについては、シミュレーション結果をみて調整します。
    　表２　に変換後の特性パラメータ推定値例を示します。
    表２　変換後の特性パラメータの推定値例
    No特性仕様記号値単位計算式
    1推力/電流Ka24000Kg*mm/(s^2*A)Ka=1000*Pmax/Imax
    2移動質量M40kgー
    3摩擦抵抗Ff8000kg*mm/s^2Ff=1000*Ffo
    4分解能dx0.00005mmー


  5. 　非線形フィードバック制御
    　前記の計算式は偏差と速度に比例した電流をフィードバックした線形フィードバック制御になっています。線形以外の制御を一般に非線形制御といいますが無限にバリエーションがあります。
    　ここでは、応答特性の改善に効果がありそうな非線形制御例を検討します。
    （１）リニアーエンコーダの分解能限界による制御不感帯の改善検討。
    　低コストXYステージにおいては、一般に高価なレーザ測長機を適用することは、コスト的に困難です。従って多くの場合、リニアーエンコーダが使用されます。
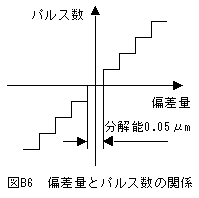
    　リニアーエンコーダのパルスの応答性には限界があり、最高速度を360mmとすると分解能は0.05μm程度となります。
    　実際の偏差と検出パルス数の関係は図B6に示すように変化します。この結果を単純に線形フィードバックすると制御電流も図B7のように相似形になります。

    　図B7に示すように制御電流がゼロとなる範囲が分解能0.05μmの範囲で存在します。これでは分解能の範囲のどこで位置が安定するかがわかりません。
    　これは、独特の要求仕様かもしれませんが、移動ステップは最小分解能でよいのですが、停止位置での安定性は必要です。
    　この要求に合わせた制御方法が必要です。（非線型制御は、要求に合わせたカスタマイズです。）
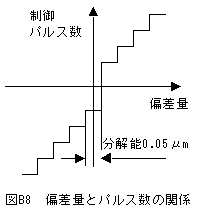
    　ここで偏差量(X)、パルス数(Pn)、制御パルス量(CP)を下記関係式で決定します。
    　If(Pn > 0)の場合
    　CP=Pn+Op/2 ----(3)式
    　If(Pn <= 0)の場合
    　CP=Pn-（1+Op/2) ----(4)式
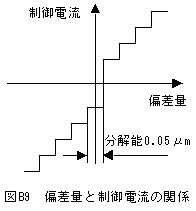
    (3)(4)式のOpは0以上の任意の実数です。今仮にOp=1として偏差量と制御パルス量の関係をグラフにすると図B8に示すようになります。
    　同様に偏差量と制御電流の関係は図B9に示すようになります。
    　図B8、図B9に示す制御条件においては、偏差パルス数がゼロの場合、制御パルス数は強制的にマイナスに変換されます。また偏差パルス数が1の場合はプラスになります。
    　この様な制御を行った場合、制御電流がゼロとなる領域がなくなり、常にプラスマイナスの高周波制御電流となりますが、移動部は質量があるため制御電流の変化に追従できずに電流の振動中心で停止します。

  6. 　計算の実行
    　VBAソフト「ｽﾃｰｼﾞ2.xls」をダブルクリックして起動した後、 シート「デェフォルト条件」の条件表の内容をシート「IN_FM」にコピーします。
    次にシート「操作」の「計算実行」ボタンを押します。
    計算結果の概要が表示されます。

    デフォルト条件表
    No記号値単位説明
    1Cm0整数制御方式の切り替え、Cm=0線形制御、Cm=1非線形制御
    2Op50パルス非線形制御のオフセット量、単位(パルス)、線形制御時無効
    3Ka24000Kg*mm/(s^2*A)リニアーモータの推力（推力/電流）、単位(Kg*mm/(s^2*A))
    4dx0.00005mmリニアーエンコーダ検出分解能、単位(mm)
    5M40kgテーブルの移動部質量、単位(kg)
    6Ff8000kg*mm/s^2摩擦抵抗、単位(kg*mm/s^2)
    7Ks300A/mm変位フィードバックゲイン、単位(A/mm)
    8Kv0A*s/mm速度フィードバックゲイン、単位(A*s/mm)
    9A00A指令電流（目標設定）、単位(A)
    10Y[0]0.005mm移動部変位初期値、単位(mm)
    11Y[1]0mm/s移動部速度初期値、単位(mm/s)
    12h0.000001s計算時間間隔、単位(s)（計算時間が長くなりますが小さくしたほうが精度がよい。）
    13N100000整数計算回数（整数）（計算時間間隔×計算回数でトータル時間）
    14Np1000整数計算結果の出力間隔回数（整数）（計算結果を全て出力すると見苦しくなるため間引きをします。）

  7. 　デフォルト条件計算結果
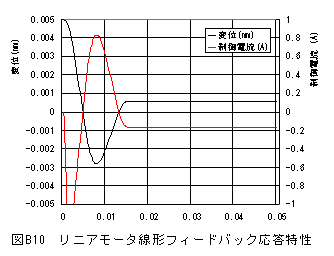
    　デフォルト条件計算結果を図B10に示します。
    　図B10は線形フィードバックの応答特性計算結果例で、デフォルト条件においては、摩擦力のため 収束時にオフセット誤差が発生しています。
    　制御電流はオフセット誤差に比例した電流が流れていますが、この制御電流で生じる推力では摩擦力 に打勝つことができず静止状態となります。

  8. 　非線形制御の応答特性計算
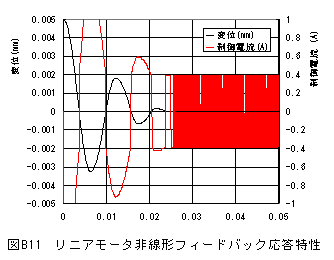
    　非線形制御の応答特性を計算するにはNo1:Cm=1(非線形制御)を設定します。
    　また非線形制御の場合、制御電流が高周波でスイッチングされるため、正確なグラフを 作成するためにNo14:Np=100に変更し出力間隔を細かくします。
    　上記の変更を行なった計算結果を図B11に示します。
    　図B11からわかるように制御電流は収束後も高周波でスイッチングされますが、移動ステージは 制御電流のスイッチングに追従せずにオフセット0の位置で静止状態となります。

    　本モデルは全ての構造体が剛体で運動質量に対して固定質量が十分大きい理想的なリニアモータ XYステージを前提としています。
    　このような理想条件においては、線形制御・非線形制御にかかわらず高速・高精度の制御条件が 存在します。
    　
    　実際には、構造体は剛体ではなく弾性体です。また固定質量は無限大では無いため、実際のXY ステージの応答特性とは食い違いを生じます。
  9. 移動/固定質量比考慮のリニアーモータXYテーブルの応答特性に行く。

トップページに戻る。