計算方法係数が実数の高次代数方程式にはベアストウ法（別名ヒッチコック法）が有効な数値計算手法です。実係 数高次代数方程式を
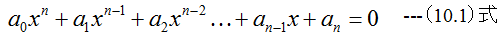
とする。ここで2つの実数pとqを用いて
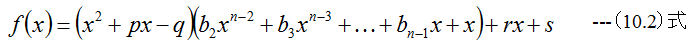
のように書ける。剰余項rx+sがゼロになるようにpとqを求めることができればf(x)は因数分解できたことに なります。続いてｘ2+px+q=0を解けば、f(x)=0を満たす２つの解を得ることができます。同様な操作を繰り返 すと全ての解を求めることができます。
（10.2）式において剰余項のｒとsは
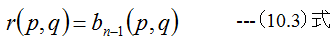
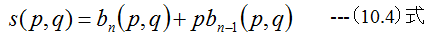
となります。（10.3）式と（10.4）式をΔpとΔqで展開してゼロとすると
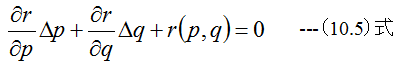
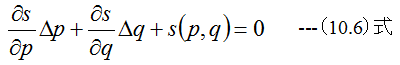
すなわち
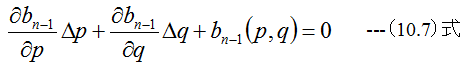
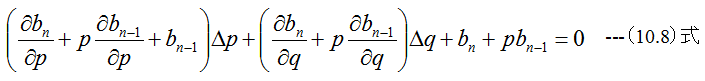
（10.7）式と（10.8）式の連立1次方程式からΔpとΔqを求め、次のpとqの値を決定します。これをヒッチコ ック法またはベアストウ法といいます。これは実質的に２元ニュートン法と同じ計算になります。
具体的なベアストウ法（ヒッチコック法）の数値計算の手法を以下に示します。
手順1 以下とします。
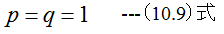
手順2 以下とします。
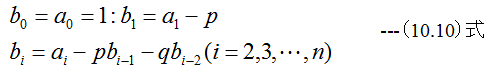
手順3 以下とします。
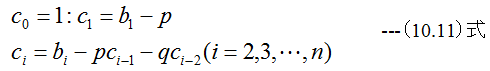
解説1 これより
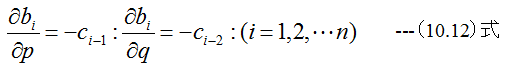
したがって
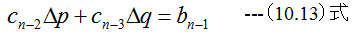
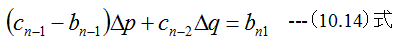
となります。
手順4 以下とします。
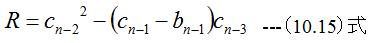
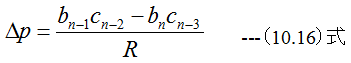
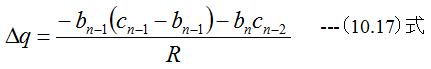
手順5 新しいp,qを次式で計算します。
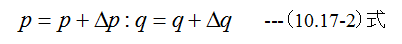
手順6 十分小さいεに対して
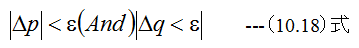
ならば手順7に進みます。さもなければ手順2から繰り返します。
手順7 2次方程式x2+px+q=0を解く
2次方程式は簡単にとけるのですがここでは、計算誤差低減のため以下の式で計算します。
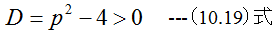
の場合
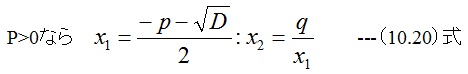
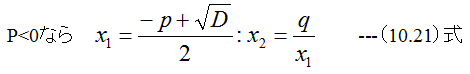
手順8
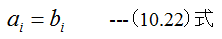
（10.22）式の定数入れ替えを行った後、手順1から繰り返します。
高次代数方程式xls(フリーソフト)のダウンロード- ダウンロード
下記の[高次代数方程式.xls(フリーソフト)]をダウンロードしてください。
ダウンロード後はダブルクリックで解凍してから使用してください。
[高次代数方程式.xls(フリーソフト)]をダウンロードする。
- 高次代数方程式.xls(フリーソフト)
- ファイル構成
（１） 補間表自動作成.xls ：フリーソフトです。
（２）シート「Sheet1」：計算条件の設定と計算結果の出力を行います。
- 注意事項
（１）ファイルの保存場所の制限はありません。
- 標準的な実行方法
（１）「高次代数方程式.xls」をダブルクリックで起動します。
（マクロを有効にして開いてください！！）
（２）収束判定値 、収束エラー判定回数、方程式次数、方程式係数を設定します。
（３）「計算実行」ボタンを押します。
（４）計算結果が表示されます。
プログラムリストVBAのプログラムリストは以下のようになります。
Dim A(101), B(101), C(101), RE(101), IM(101)
Dim M, PP, QQ, CT, ZZ, DP, DQ, EPS, ERR, EN
Sub Main()
'初期化
ERR = 0
For i = 0 To 100
Sheets("Sheet1").Cells(12 + i, 6).Formula = ""
Sheets("Sheet1").Cells(12 + i, 7).Formula = ""
Next i
'初期入力
EPS = Sheets("Sheet1").Cells(9, 3).Value
EN = Sheets("Sheet1").Cells(10, 3).Value
N = Sheets("Sheet1").Cells(11, 3).Value
For i = 0 To N
A(i) = Sheets("Sheet1").Cells(12 + i, 3).Value
RE(i) = 0: IM(i) = 0
Next i
M = N
BEGIN
Sheets("Sheet1").Cells(10, 6).Value = CT
If ERR = 1 Then
Sheets("Sheet1").Cells(13, 6).Formula = "エラー"
Else
For i = 1 To N
Sheets("Sheet1").Cells(12 + i, 6).Value = RE(i)
Sheets("Sheet1").Cells(12 + i, 7).Value = IM(i)
Next i
End If
End Sub
Sub BEGIN()
Do Until M = 0
If M = 1 Then RE(M) = -A(1): Exit Do
PP = 1: QQ = 1
CT = 0
AA = A(0)
For i = 0 To M
A(i) = A(i) / AA
Next i
If M = 2 Then
PP = A(1): QQ = A(2)
Else
REPEAT
End If
QUADRATIC
M = M - 2
For i = 1 To M
A(i) = B(i)
Next i
Loop
End Sub
Sub REPEAT()
Do
CT = CT + 1
B(0) = 1
B(1) = A(1) - PP
B(2) = A(2) - PP * B(1) - QQ
For J = 3 To M
B(J) = A(J) - PP * B(J - 1) - QQ * B(J - 2)
Next J
C(0) = 1
C(1) = B(1) - PP
C(2) = B(2) - PP * C(1) - QQ
For J = 3 To M - 1
C(J) = B(J) - PP * C(J - 1) - QQ * C(J - 2)
Next J
ZZ = C(M - 2) ^ 2 - C(M - 3) * (C(M - 1) - B(M - 1))
DP = (C(M - 2) * B(M - 1) - C(M - 3) * B(M)) / ZZ
DQ = (C(M - 2) * B(M) - B(M - 1) * (C(M - 1) - B(M - 1) - B(M - 1))) / ZZ
PP = PP + DP: QQ = QQ + DQ
If CT > EN Then ERR = 1: Exit Do
Loop Until Abs(DP) < EPS And Abs(DQ) < EPS
End Sub
Sub QUADRATIC()
DD = PP ^ 2 - 4 * QQ
B1 = -0.5 * PP
B2 = Sqr(Abs(DD)) * 0.5
RE(M) = B1: RE(M - 1) = B1
If DD <= 0 Then
IM(M) = B2: IM(M - 1) = -B2
Else
If PP > 0 Then B2 = -B2
RE(M) = B1 + B2
RE(M - 1) = QQ / RE(M)
End If
End Sub
１１章：ラグランジュ補間多項式に行く。