計算方法n個の関数値yi=f(xi)(i=1,2,‥‥,n)が与えられるとき、ラグランジュ補間多項式は次のように記載されます。
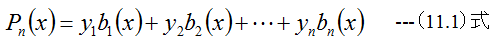
（11.1）式において、bi(x)はｎ-1次の多項式です。bi(x)は下記式で決定されます。
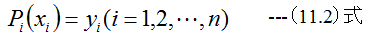
（11.2）式を（11.1）式に代入すると
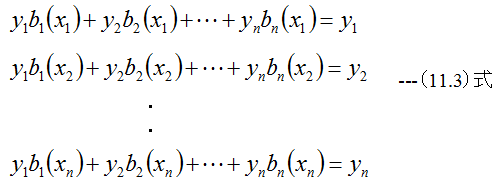
となります。ここでbi(x)がx1,x2,‥‥,xnにおいて
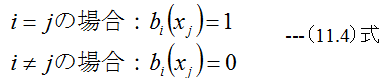
とするならば、（11.3）式を満足することになります。（11.4）式を具体的な関数形にすると
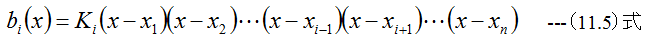
となります。（11.5）式で注意すべきは(x-xi）の項が無い点です。定数Kiはx=xiにおいて、bi（x)=1の条件から
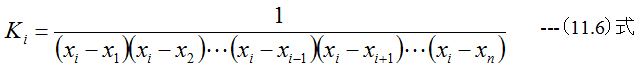
となります。従って
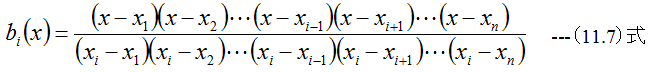
となります。（11.1）式に（11.7）式を代入すると
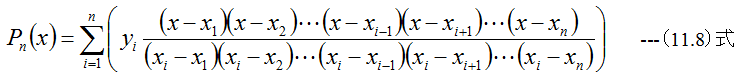
となります。（11.8）式は一見、計算が面倒に見えますが、単純繰り返しの計算ですのでプ ログラム的には難しくありません。
ラグランジュxls(フリーソフト)のダウンロード- ダウンロード
下記のラグランジュ.xls(フリーソフト)]をダウンロードしてください。
ダウンロード後はダブルクリックで解凍してから使用してください。
[ラグランジュ.xls(フリーソフト)]をダウンロードする。
- ラグランジュ.xls(フリーソフト)
- ファイル構成
（１） ラグランジュ.xls ：フリーソフトです。
（２）シート「Sheet1」：計算条件の設定を行います。
（２）シート「Sheet2」：計算結果の出力されます。
- 注意事項
（１）ファイルの保存場所の制限はありません。
- 標準的な実行方法
（１）「ラグランジュ.xls」をダブルクリックで起動します。
（マクロを有効にして開いてください！！）
（２）初期値ｘ0、間隔ｄｘ、回数N、データ数NiとデータXiとYiをを設定します。
（３）「計算実行」ボタンを押します。
（４）計算結果がシート「Sheet2」に表示されます。
プログラムリストVBAのプログラムリストは以下のようになります。
Dim Xi(1001), Yi(1001), B(1001)
Sub Main()
Sheets("Sheet2").Select
Cells.Select
Selection.Clear
'初期入力
x0 = Sheets("Sheet1").Cells(3, 2).Value
dx = Sheets("Sheet1").Cells(4, 2).Value
N = Sheets("Sheet1").Cells(5, 2).Value
Ni = Sheets("Sheet1").Cells(8, 2).Value
For i = 1 To Ni Step 1
Xi(i) = Sheets("Sheet1").Cells(9 + i, 2).Value
Yi(i) = Sheets("Sheet1").Cells(9 + i, 3).Value
Next i
'タイトル
Sheets("Sheet2").Cells(1, 1).Formula = "No"
Sheets("Sheet2").Cells(1, 2).Formula = "x"
Sheets("Sheet2").Cells(1, 3).Formula = "補間y"
'表作成
For k = 0 To N Step 1
Y = 0
X = x0 + dx * k
For i = 1 To Ni Step 1
B(i) = 1
For j = 1 To Ni Step 1
If j = i Then
Else
B(i) = B(i) * (X - Xi(j)) / (Xi(i) - Xi(j))
End If
Next j
Y = Y + B(i) * Yi(i)
Next i
Sheets("Sheet2").Cells(2 + k, 1).Value = k
Sheets("Sheet2").Cells(2 + k, 2).Value = X
Sheets("Sheet2").Cells(2 + k, 3).Value = Y
Next k
End Sub
補間精度の検証基礎データ表を下記の条件で作成し補間精度の検証を行います。
基礎データ表作成方程式 ｙ=SIN(ｘ)+SIN(ｘ/3)
x値の間隔 ｄｘ＝0.4
ｘの最大値 xmax＝3.6
欠如ｘ値＝1.2（意図的に削除しました。）
補間表作成条件
初期値ｘ0=0
間隔ｄｘ=0.05
回数N=72
この条件では、関係式がわかっているため補間誤差を容易に計算できます。計算結果を図11-1に示します。
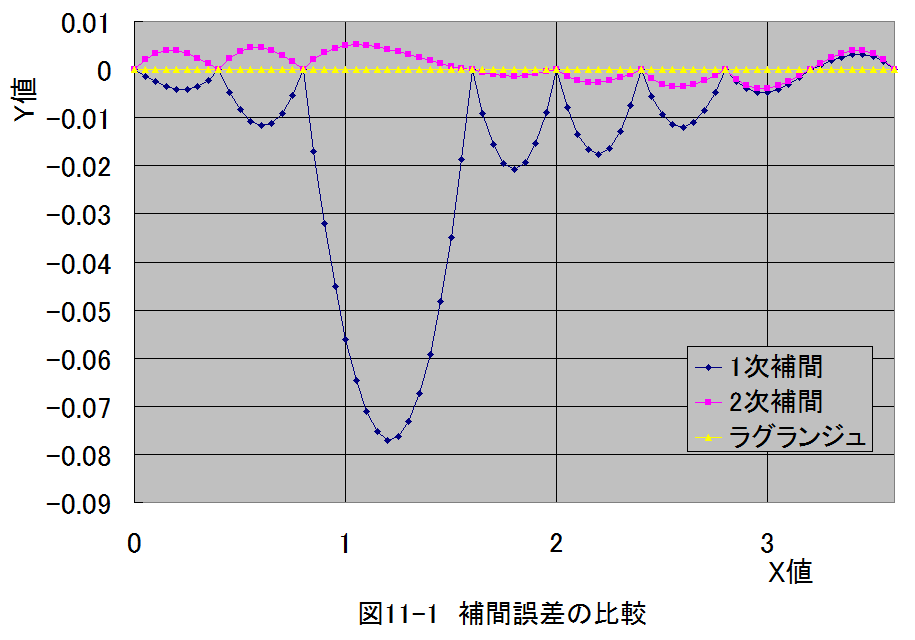
図11-1から、ラグランジュ、2次補間、1次補間の順に補間誤差が小さいことがわかります。計算量も同じ順序となります。しかし、現在のパソコンは性能が向上しているため、計算時間はあまり問題となりません。
しかし、2次補間、1次補間はEXCELワークシート関数で計算できますが、ラグランジュはワークシート関数での計算に適しません。VBAでのプログラミングが有効です。単純計算の繰り返しのため、プログラミングは容易です。
１２章：偏微分方程式（ラプラスの方程式）に行く。