ラプラスの方程式は
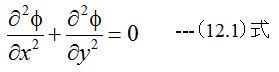
で与えられる偏微分方程式です。今任意の関数φ(x,y)を考え、微小量hだけ位置を変化させた場合
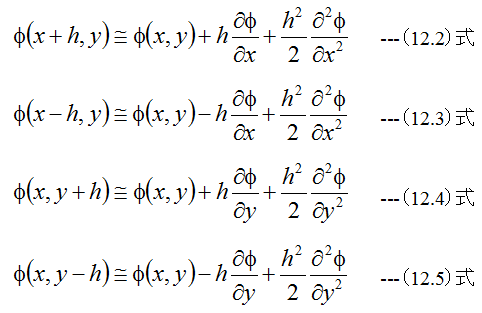
が成立します。(12.2)式から(12.5)式を加算すると
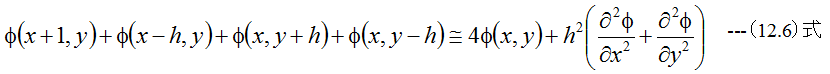
となります。ここで、(12.1)式と(12.6)式から
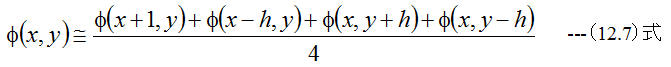
の関係式が得られます。しかし、(12.7)式は近似式であり正確ではありません。このため新しいφをφ'とし
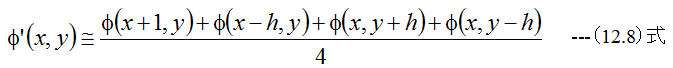
(12.8)式の計算を繰り返すことにより、誤差を低減する必要があります。また(12.8)式が成立するには、xの変化量hとyの変化量hが等しい必要があります。
(12.8)式の計算を実行するには、計算領域より小さい方向と大きい方向にひとつ余分な値を設定する必要があります。
この設定が境界条件です。境界条件の設定無しには(12.8)式の実行はできません。(12.1)式の解は無限に存在し、境界条件を設定しないと値が決定できません。
偏微分方程式はひとつの条件を規定しますが、変数が多数あるため厳密に境界条件を規定する必要があります。偏微分方程式が難解なのは、厳密に境界条件を規定する必要があるためです。
- ダウンロード
下記の偏微分方程式1.xls(フリーソフト)]をダウンロードしてください。
ダウンロード後はダブルクリックで解凍してから使用してください。
 [偏微分方程式1.xls(フリーソフト)]をダウンロードする。
[偏微分方程式1.xls(フリーソフト)]をダウンロードする。
- 偏微分方程式1.xls(フリーソフト)
- ファイル構成
(1) 偏微分方程式1.xls :フリーソフトです。
(2)シート「Sheet1」:計算条件の設定を行います。
(2)シート「Sheet2」:計算結果の出力されます。
- 注意事項
(1)ファイルの保存場所の制限はありません。
- 標準的な実行方法
(1)「偏微分方程式1.xls」をダブルクリックで起動します。
(マクロを有効にして開いてください!!)
(2)行数(j)、列数(j)、変化幅、収束判定値、最大演算回数、演算領域指定を設定します。
(3)境界条件表を設定します。(最外周は全て 境界条件とする必要があります。)
(4)境界条件表の最大は100×100です。
(5)演算領域の初期値は境界条件(i=0,j=0)と同じ値に自動設定されます。
(6)「計算実行」ボタンを押します。
(7)計算結果がシート「Sheet2」に表示されます。
VBAのプログラムリストは以下のようになります。
Dim T(101, 101), DT(101, 101), C(101, 101)
Sub Main()
'Sheet2クリア
Sheets("Sheet2").Select
Cells.Select
Selection.Clear
'初期入力
Ni = Sheets("Sheet1").Cells(4, 3).Value
Nj = Sheets("Sheet1").Cells(5, 3).Value
h = Sheets("Sheet1").Cells(6, 3).Value
e = Sheets("Sheet1").Cells(7, 3).Value
Nc = Sheets("Sheet1").Cells(8, 3).Value
Ce = Sheets("Sheet1").Cells(9, 3).Value
'計算部分
For i = 0 To Ni - 1 Step 1
For j = 0 To Nj - 1 Step 1
F = Sheets("Sheet1").Cells(15 + i, 2 + j).Value
If F = Ce Then
C(i, j) = 1
T(i, j) = T(0, 0)
Else
C(i, j) = 0
T(i, j) = F
End If
Next j
Next i
For k = 0 To Nc Step 1
Nk = 0
Se = 0
For i = 0 To Ni - 1 Step 1
For j = 0 To Nj - 1 Step 1
If C(i, j) = 1 Then
DT(i, j) = (T(i - 1, j) + T(i + 1, j) + T(i, j - 1) + T(i, j + 1)) / 4
Nk = Nk + 1
Se = Se + Abs(DT(i, j) - T(i, j))
Else
End If
Next j
Next i
For i = 0 To Ni - 1 Step 1
For j = 0 To Nj - 1 Step 1
If C(i, j) = 1 Then T(i, j) = DT(i, j)
Next j
Next i
'収束状況出力
Sheets("Sheet2").Cells(5 + k, 1).Value = k
Sheets("Sheet2").Cells(5 + k, 2).Value = Se / Nk
If Se / Nk < e Then Exit For
Next k
'結果出力
Sheets("Sheet2").Cells(1, 1).Formula = "計算結果"
Sheets("Sheet2").Cells(4, 1).Formula = "計算回数"
Sheets("Sheet2").Cells(4, 2).Formula = "変化量"
For j = 0 To Nj - 1 Step 1
Sheets("Sheet2").Cells(4, 4 + j).Value = j
Next j
For i = 0 To Ni - 1 Step 1
Sheets("Sheet2").Cells(5 + i, 3).Value = i
For j = 0 To Nj - 1 Step 1
Sheets("Sheet2").Cells(5 + i, 4 + j).Value = T(i, j)
Next j
Next i
End Sub
偏微分方程式1(ラプラスの方程式)(温度分布の計算)
計算条件
| 項目 | 記号 | 値 |
| 行数(j) | Ni | 21 |
| 列数(j) | Nj | 21 |
| 変化幅 | h | 1 |
| 収束判定値 | e | 0.01 |
| 最大演算回数 | Nc | 400 |
| 演算領域指定 | Ce | -99 |
*境界条件表(最大100×100まで)
| - | j=0 | j=1 | j=2 | j=3 | j=4 | j=5 | j=6 | j=7 | j=20 | j=8 | j=9 | j=10 | j=11 | j=12 | j=13 | j=14 | j=15 | j=16 | j=17 | j=18 | j=20 |
| i=0 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 |
| i=1 | 300 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | 300 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | 300 |
| i=2 | 300 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | 300 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | 300 |
| i=3 | 300 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | 300 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | 300 |
| i=4 | 300 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | 300 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | 300 |
| i=5 | 300 | -99 | -99 | 600 | 600 | 550 | -99 | -99 | 300 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | 300 |
| i=6 | 300 | -99 | -99 | 600 | 600 | 550 | -99 | -99 | 300 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | 300 |
| i=7 | 300 | -99 | -99 | 600 | 600 | 550 | -99 | -99 | 300 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | 300 |
| i=8 | 300 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | 300 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | 300 |
| i=9 | 300 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | 300 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | 300 |
| i=10 | 300 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | 300 | -99 | -99 | 0 | 0 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | 300 |
| i=11 | 300 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | 300 | -99 | -99 | 0 | 0 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | 300 |
| i=12 | 300 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | 300 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | 300 |
| i=13 | 300 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | 300 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | 300 |
| i=14 | 300 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | 300 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | 300 |
| i=15 | 300 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | 300 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | 300 |
| i=16 | 300 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | 300 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | 300 |
| i=17 | 300 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | 300 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | 300 |
| i=18 | 300 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | 300 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | 300 |
| i=19 | 300 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | 300 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | -99 | 300 |
| i=20 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 |
計算結果
*計算回数毎の変化量が表示されます
| 計算回数 | 変化量 |
| 0 | 4.13074712643678 |
| 1 | 3.09806034482759 |
| 2 | 2.74784482758621 |
| 3 | 2.36900592672414 |
| 4 | 2.10901019216954 |
| 5 | 1.87704152074353 |
| 6 | 1.69420790398258 |
計算結果表
| - | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 20 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 20 |
| 0 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 |
| 1 | 300 | 312 | 324 | 332 | 335 | 333 | 328 | 322 | 300 | 315 | 309 | 304 | 300 | 298 | 296 | 295 | 295 | 296 | 297 | 298 | 300 |
| 2 | 300 | 326 | 350 | 368 | 374 | 370 | 358 | 344 | 300 | 329 | 317 | 306 | 299 | 294 | 291 | 290 | 290 | 292 | 293 | 295 | 300 |
| 3 | 300 | 343 | 383 | 415 | 425 | 414 | 391 | 365 | 300 | 341 | 322 | 306 | 296 | 289 | 285 | 284 | 285 | 287 | 289 | 293 | 300 |
| 4 | 300 | 362 | 425 | 484 | 495 | 471 | 426 | 384 | 300 | 350 | 322 | 302 | 288 | 280 | 276 | 275 | 277 | 281 | 285 | 290 | 300 |
| 5 | 300 | 380 | 472 | 600 | 600 | 550 | 459 | 397 | 300 | 351 | 316 | 291 | 275 | 266 | 263 | 265 | 268 | 274 | 280 | 286 | 300 |
| 6 | 300 | 385 | 482 | 600 | 600 | 550 | 462 | 393 | 300 | 340 | 300 | 271 | 254 | 247 | 247 | 251 | 258 | 266 | 274 | 283 | 300 |
| 7 | 300 | 380 | 471 | 600 | 600 | 550 | 446 | 373 | 300 | 317 | 272 | 239 | 223 | 220 | 226 | 236 | 247 | 258 | 269 | 279 | 300 |
| 8 | 300 | 362 | 424 | 480 | 487 | 456 | 397 | 338 | 300 | 282 | 232 | 192 | 178 | 185 | 201 | 218 | 235 | 250 | 263 | 276 | 300 |
| 9 | 300 | 343 | 382 | 410 | 413 | 391 | 350 | 299 | 300 | 242 | 180 | 121 | 110 | 142 | 174 | 202 | 224 | 243 | 259 | 274 | 300 |
| 10 | 300 | 328 | 351 | 365 | 363 | 345 | 311 | 265 | 300 | 206 | 126 | 0 | 0 | 98 | 153 | 190 | 217 | 238 | 256 | 272 | 300 |
| 11 | 300 | 316 | 329 | 335 | 331 | 314 | 286 | 245 | 300 | 192 | 117 | 0 | 0 | 95 | 151 | 188 | 216 | 238 | 256 | 272 | 300 |
| 12 | 300 | 309 | 315 | 316 | 310 | 295 | 271 | 239 | 300 | 198 | 149 | 101 | 96 | 132 | 167 | 196 | 220 | 240 | 257 | 272 | 300 |
| 13 | 300 | 304 | 306 | 304 | 297 | 285 | 266 | 241 | 300 | 212 | 182 | 158 | 153 | 168 | 189 | 209 | 229 | 246 | 261 | 275 | 300 |
| 14 | 300 | 301 | 300 | 297 | 291 | 280 | 266 | 248 | 300 | 228 | 209 | 195 | 191 | 198 | 210 | 224 | 239 | 253 | 265 | 277 | 300 |
| 15 | 300 | 299 | 298 | 294 | 288 | 280 | 269 | 256 | 300 | 242 | 230 | 221 | 219 | 222 | 229 | 239 | 250 | 261 | 271 | 281 | 300 |
| 16 | 300 | 299 | 297 | 293 | 288 | 282 | 274 | 265 | 300 | 256 | 248 | 242 | 240 | 242 | 247 | 253 | 261 | 269 | 277 | 285 | 300 |
| 17 | 300 | 298 | 297 | 294 | 290 | 286 | 280 | 274 | 300 | 268 | 263 | 259 | 258 | 259 | 262 | 266 | 271 | 277 | 283 | 288 | 300 |
| 18 | 300 | 299 | 297 | 295 | 293 | 290 | 286 | 283 | 300 | 279 | 276 | 274 | 273 | 273 | 275 | 278 | 281 | 285 | 288 | 292 | 300 |
| 19 | 300 | 299 | 299 | 298 | 296 | 295 | 293 | 291 | 300 | 290 | 288 | 287 | 287 | 287 | 288 | 289 | 291 | 292 | 294 | 296 | 300 |
| 20 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 |
計算結果グラフ
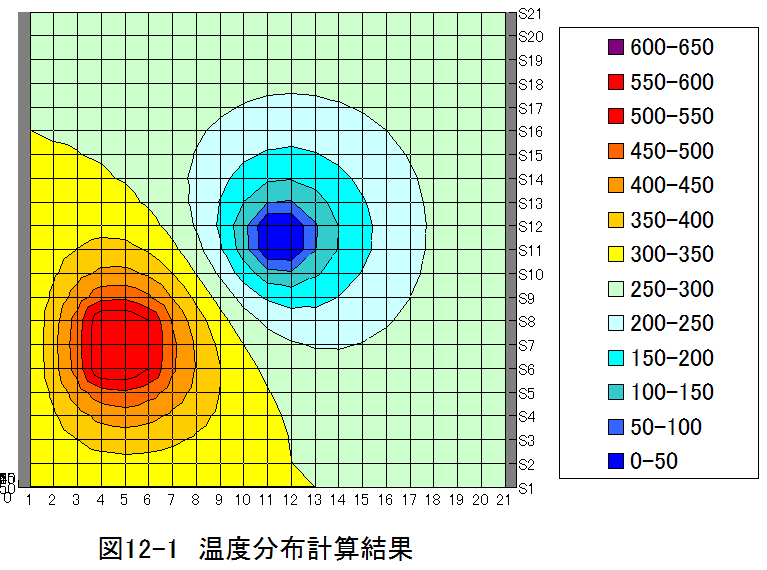
偏微分方程式(ラプラスの方程式)は温度分布や電圧分布を与える基礎方程式です。 数値計算でほとんどの条件の分布状態を求めることが可能なことがわかります。