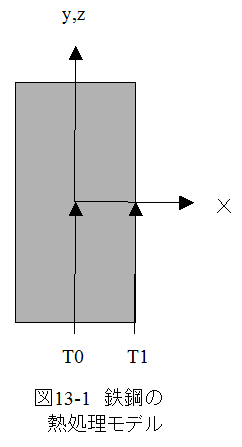
1次元熱伝導のモデル図13-1に鉄鋼板の熱処理モデルを示します。図13-1において、板厚方向をｘとします。またyz方向は十分大きいとします。
鉄鋼板の熱処理においては、まず鉄鋼を高温炉で十分過熱します。十分な過熱時間後は鉄鋼全体が均一な温度に上昇します。
過熱完了後、冷水につけて急冷します。ここでは、冷水は十分な量があり冷水の温度上昇は無視できるとします。この仮定において鉄鋼表面は瞬間的に冷水温度になると仮定できます。
鉄鋼中心部は温度T0から時間がかかってT1温度になっていぐとかんがえられます。
ここで、中心点においては左右対称の関係から温度勾配dφ/dx=0が成立することが予想できます。
境界条件としては
（１）時間ｔ＝0において：表面を除く温度＝T0、表面温度＝T1
（２）全ての時間tのX=0において温度勾配dφ/dx=0
が成立することがわかります。
1次元熱伝導方程式1次元熱伝導方程式は
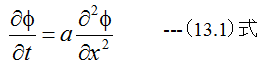
で与えられます。（13.1）式において、φが温度、ｔが時間、xが中心からの距離です。aは熱伝導率/体積熱容 量で温度伝導率といいます。基本単位はm2/sですが、計算の都合上mm2/sを用います。
鉄鋼の温度伝導率は20.3mm2/s、銅の温度伝導率は112.5mm2/sとなります。
1次元熱伝導方程式の計算方法今任意の関数φ(x,ｔ)を考え、微小量Δxだけ位置を変化させた場合
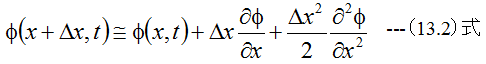
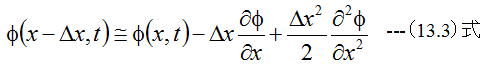
が成立します。（13.2）と（12.3）式を加算すると
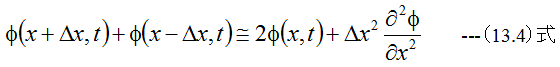
となります。また関数φ(x,ｔ)を考え、微小量Δｔだけ位置を変化させた場合
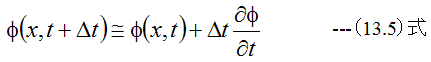
の関係式が得られます。（13.1）式に（13.4）式と（13.5）式を代入して整理すると
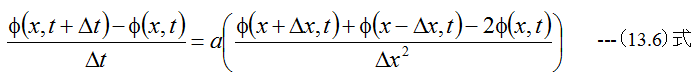
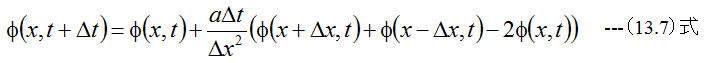
（13.7）式が得られます。（13.7）式によれば、Δｔ時間後のΦの値を次々と計算できるこ とがわかります。ただし（13.7）式が成立するためには、以下の条件式を満足するようにΔｔ の値を設定する必要があります。
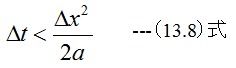
境界条件と（13.7）式、（13.8）式から1次元熱伝導方程式を解くことができます。
1次元熱伝導方程式.xls(フリーソフト)のダウンロード- ダウンロード
下記の1次元熱伝導方程式.xls(フリーソフト)]をダウンロードしてください。
ダウンロード後はダブルクリックで解凍してから使用してください。
[1次元熱伝導方程式.xls(フリーソフト)]をダウンロードする。
- 1次元熱伝導方程式.xls(フリーソフト)
- ファイル構成
（１） 1次元熱伝導方程式.xls ：フリーソフトです。
（２）シート「Sheet1」：計算条件の設定と計算結果の出力を行います。
（２）シート「Sheet2」：計算結果をグラフ化します。
- 注意事項
（１）ファイルの保存場所の制限はありません。
- 標準的な実行方法
（１）「1次元熱伝導方程式.xls」をダブルクリックで起動します。
（マクロを有効にして開いてください！！）
（２）温度伝導率、板厚、過熱温度、冷却温度、板厚刻み回数、時間刻み、時間計算回数を設定します。
（３）その他の境界条件はプログラム内で自動設定されるため変更できません。
（６）「計算実行」ボタンを押します。
（7）計算結果がシート「Sheet1」に表示されます。
プログラムリストVBAのプログラムリストは以下のようになります。
Dim T(101), OT(101)
Sub Main()
'初期入力
N = Sheets("Sheet1").Cells(8, 3).Value
T0 = Sheets("Sheet1").Cells(6, 3).Value
T1 = Sheets("Sheet1").Cells(7, 3).Value
A = Sheets("Sheet1").Cells(4, 3).Value
DT = Sheets("Sheet1").Cells(10, 3).Value
DX = Sheets("Sheet1").Cells(9, 3).Value
Nt = Sheets("Sheet1").Cells(11, 3).Value
C = A * DT / DX ^ 2
'初期設定
For i = 0 To N - 1
T(i) = T0
Sheets("Sheet1").Cells(15, 2 + i).Value = T(i)
Next i
T(N) = T1
'表題と1行目出力
Sheets("Sheet1").Cells(14, 1).Formula = "時間(s)"
Sheets("Sheet1").Cells(15, 1).Value = 0
For i = 0 To N
Sheets("Sheet1").Cells(14, 2 + i).Formula = DX * i & "(mm)"
Sheets("Sheet1").Cells(15, 2 + i).Value = T(i)
Next i
'繰り返し計算
For j = 1 To Nt
For i = 0 To N
OT(i) = T(i)
Next i
T(0) = T(0) + C * (OT(1) - 2 * OT(0) + OT(0))
For i = 1 To N - 1
T(i) = T(i) + C * (OT(i + 1) - 2 * OT(i) + OT(i - 1))
Next i
'結果出力
Sheets("Sheet1").Cells(15 + j, 1).Value = DT * j
For i = 0 To N
Sheets("Sheet1").Cells(15 + j, 2 + i).Value = T(i)
Next i
Next j
End Sub
サンプル条件の実行結果計算条件
| 項目 | 記号 | 値 | 単位 |
| 温度伝導率 | a | 20.28 | mm2/s |
| 板厚 | ｈ | 10 | mm |
| 過熱温度 | T0 | 1000 | ℃ |
| 冷却温度 | T1 | 30 | ℃ |
| 板厚刻み回数 | Nh | 5 | 回 |
| 板厚変化 | ｄｘ | 1 | ｍｍ |
| 時間刻み | ｄｔ | 0.01 | ｓ |
| 時間計算回数 | Nt | 500 | 回 |
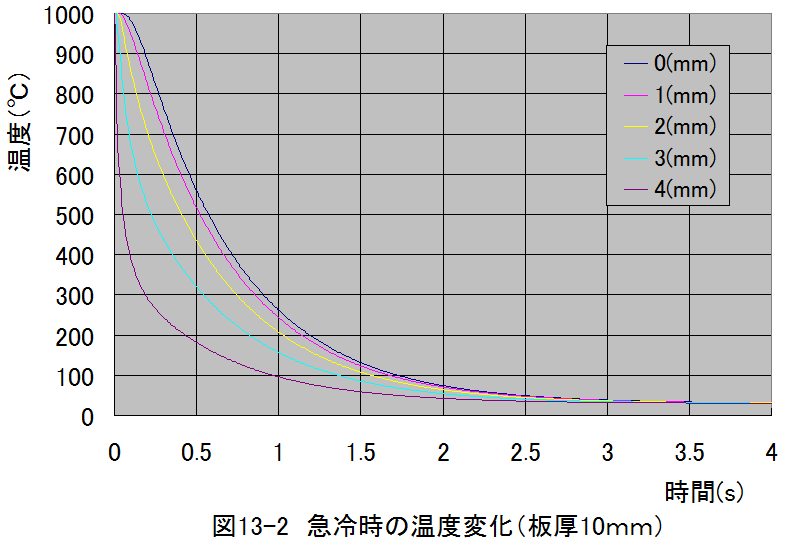
計算結果グラフ
計算条件
| 項目 | 記号 | 値 | 単位 |
| 温度伝導率 | a | 20.28 | mm2/s |
| 板厚 | ｈ | 20 | mm |
| 過熱温度 | T0 | 1000 | ℃ |
| 冷却温度 | T1 | 30 | ℃ |
| 板厚刻み回数 | Nh | 5 | 回 |
| 板厚変化 | ｄｘ | 1 | ｍｍ |
| 時間刻み | ｄｔ | 0.01 | ｓ |
| 時間計算回数 | Nt | 500 | 回 |
計算結果グラフ
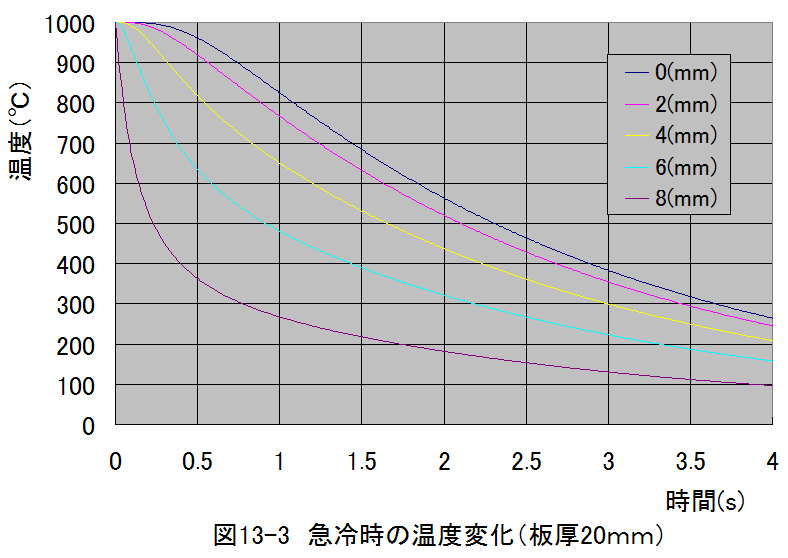
図13-2 と図13-3から中心部(x=0)は冷却が表面部より遅れることがわか ります。また、板厚が厚くなると急激に冷却が遅くなります。
これから、板厚の厚い鉄鋼の熱処理は難しいことが理解できます。逆にカミ ソリのように薄い材料は急激な冷却が可能であることがわかります。
１４章：1次元波動方程式に行く。