工場の生産計画を例にとると製品群xj(j=1,…,n)があり、各製品の利益をcj(j=1,…,n)とするならば、合計の利益zは
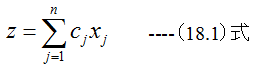
となります。
各製品は無限に生産できるわけではなく、所有している機械群bi(i=1,…..,m)の生産能力に依存します。各製品xj(j=1,…,n)が機械群bi(i=1,…..,m)を 占有する能力をaij(i=1,…..,m)(j=1,…,n)とするならば、制約条件は以下のようになります。
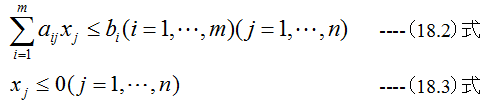
工場の生産計画を例にとると製品群xj(j=1,…,n)があり、各製品の利益をcj(j=1,…,n)とするならば、合計の利益zは しかし、線形計画法(シンプレックス法)においては
「目的関数を最大にする点は制約条件の端点にある。」
という重要な定理が成立します。例えば、最大積載量が10tのトラックで最大の輸送量は10tということになり、制約条件の限界点に目的関数を最大にする点が存在することになります。
従って、制約条件の全ての端点における目的関数の値を計算して、最大となる条件を求めれば良いことになります。
しかし、制約条件の全ての端点を種々の組合せの連立1次方程式を解く作業となり結構大変です。シンプレックス法は鮮やかな計算手法で目的関数を最大とする解を求めます。
しかし、鮮やかな計算手法ゆえにそのカラクリを理解するのは容易ではありません。
目的関数のマトリックスMAT(i,j)への設定
以下のようにマトリックスMAT(i,j)に設定します。
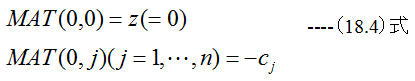
制約条件のマトリックスMAT(i,j)への設定
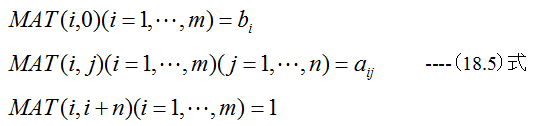
以上の操作で(n+m+1)列、(m+1)行のマトリックスが完成します。
実例におけるStep0のマトリックス
以下の実例でStep0のマトリックスを作成します。
4種類の製品T1,T2,T3,T4は3台の機械A,B,Cを使用して作られる。各製品の利益は
であり、各機械の使用時間と使用時間制限は単位 製品T1 製品T2 製品T3 製品T4 利益(万円) 4 6 10 8
上記の条件で作成されたStep0のマトリックスは機械 使用可能時間 製品T1 製品T2 製品T3 製品T4 機械A 180 1 2 3 4 機械B 150 2 1 5 2 機械C 160 1 2 3 2
工場の生産計画を例にとると製品群xj(j=1,…,n)があり、各製品の利益をcj(j=1,…,n)とするならば、合計の利益zは MAT(1,5)=MAT(2,6)=MAT(3,7)=1となっています。基底変数 制限 X1 X2 X3 X4 X5 X6 X7 -Z 0 -4 -6 -10 -8 0 0 0 X5 180 1 2 3 4 1 0 0 X6 150 2 1 5 2 0 1 0 X7 160 1 2 3 2 0 0 1
X5=MAT(1,0)=180
X6=MAT(2,0)=150
X7=MAT(3,0)=160
とするならば、目的関数の値は
Z=MAT(0,5)*X5+MAT(0,6)*X6+MAT(0,7)*X7=0(=MAT(0,0))
の関係がありそうです。
ここで、X5,X6,X7は不等式を等式に変換するための変数であり、スラック変数といいます。また、値がゼロでない変数を基底変数といいます。
Step0のマトリックスでは、X5,X6,X7がゼロでなく、X1,X2,X3,X4の値がゼロで制約条件式を満足します。
ピボット列の選定(基底に入れる変数の決定)
Step0ではスラック変数が基底変数となっているため、目的関数の値はゼロです。どの変数を基底変数に入れるかを選定する必要があります。Step0の表において
MAT(0,3)=-10
でありX3を基底変数に入れると判断します。
Min MAT(i,0)(i=1,….,m)
を満足する列を探索します。この列をピボット列(PIVOT)とします。
ピボット行の選定(基底から追い出す変数の決定)
新しく基底変数をいれるためには、旧基底変数のいずれかを追い出す必要があります。ここで
D(i)=MAT(i,0)/MAT(i,PIVOT)
の演算を行い、最小のD(i)を選択して、選択たれた基底変数を追い出します。具体的には
D(1)=MAT(1,0)/MAT(1,PIVOT) =180/3=60
D(2)=MAT(2,0)/MAT(2,PIVOT) =150/5=30
D(3)=MAT(3,0)/MAT(3,PIVOT) =160/3=53.3
となりD(2)(=X6)が生産可能数が小さいと判断され、基底変数から追い出されます。これをピボット行(ROW)とします。
基底変数の交換およびピボット演算
ピボット行のマトリックスMAT(ROW,j)の変更
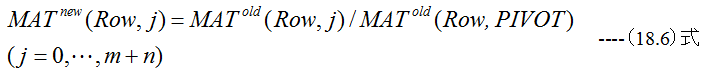
ピボット行以外のマトリックスMAT(i,j)の変更
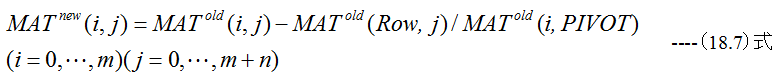
基底変数の交換およびピボット演算後のマトリックス
Step1のマトリックスは
上記の表において、基底変数にX3が加わりました。X3=30であり、Z=10*30=300となります。しかしこ れがベストではありません。MAT(0,2)=-2、MAT(0,4)=-2であり改善の余地があることを示しています。基底変数 制限 X1 X2 X3 X4 X5 X6 X7 -Z 300 0 -4 0 -4 0 2 0 X5 90 -0.2 1.4 0 2.8 1 -0.6 0 X3 30 0.4 0.2 1 0.4 0 0.2 0 X7 70 -0.2 1.4 0 0.8 0 -0.6 1
Step2のマトリックスは
となり、基底変数にX4が加わります。この操作を繰り返すと基底変数 制限 X1 X2 X3 X4 X5 X6 X7 -Z 428.571428571429 -0.285714285714286 -2 0 0 1.42857142857143 1.14285714285714 0 X4 32.1428571428571 -0.0714285714285715 0.5 0 1 0.357142857142857 -0.214285714285714 0 X3 17.1428571428571 0.428571428571429 0 1 0 -0.142857142857143 0.285714285714286 0 X7 44.2857142857143 -0.142857142857143 1 0 0 -0.285714285714286 -0.428571428571429 1
Step4で
となり、MAT(0,j)にマイナス項が無くなります。この状態がベスト解となります。従ってベスト解は X1=40、X2=50、X4=10で利益がZ=540となります。基底変数 制限 X1 X2 X3 X4 X5 X6 X7 -Z 540 0 0 1.33333333333333 0 0.666666666666667 0.666666666666667 2 X4 10 0 0 0 1 0.5 0 -0.5 X1 40 1 0 2.33333333333333 0 -0.333333333333333 0.666666666666667 0 X2 50 0 1 0.333333333333334 0 -0.333333333333333 -0.333333333333333 1
- ダウンロード
下記のシンプレックス法.xls(フリーソフト)]をダウンロードしてください。
ダウンロード後はダブルクリックで解凍してから使用してください。
 シンプレックス法.xls(フリーソフト)]をダウンロードする。
シンプレックス法.xls(フリーソフト)]をダウンロードする。
- シンプレックス法.xls(フリーソフト)
- ファイル構成
(1) シンプレックス法.xls :フリーソフトです。
(2)シート「Sheet1」:計算条件の設定と計算結果の出力を行います。
- 注意事項
(1)ファイルの保存場所の制限はありません。
- 標準的な実行方法
(1)「シンプレックス法.xls」をダブルクリックで起動します。
(マクロを有効にして開いてください!!)
(2)制約条件の数と決定変数の数を設定します。
(3)目的関数を設定します。
(4)制約条件を設定します。
(5)「計算実行」ボタンを押します。
(6)計算結果がシート「Sheet1」に表示されます。
・本プログラムは最適化計算の様子を理解するため、各ステップごとの マトリックスの値を表示しています。このため、多くの変数、制約条件数の 計算にはてきしません。 、各ステップごとのマトリックスの値の表示をやめれば、多くの変数、制約条件数 に対応しやすくなります。
VBAのプログラムリストは以下のようになります。
'M=制約条件の数
'N=決定変数の数
'MN=M+N
'MAT(0,J)=目的関数の係数
'MAT(I,0)=制約条件の限界値
'ITER=ステップの繰り返し回数
'PIBOT=ピボット列値
'ROW=ピボット行の値
Dim MAT(101, 201), VAR(100), ITER, N, M, MN
Sub Main()
'条件の読込
M = Sheets("Sheet1").Cells(4, 3).Value
N = Sheets("Sheet1").Cells(5, 3).Value
MN = M + N
For i = 0 To 100
For j = 0 To 200
MAT(i, j) = 0
Next j
Next i
For i = 1 To M
For j = 0 To N
MAT(i, j) = Sheets("Sheet1").Cells(13 + i, 2 + j).Value
Next j
MAT(i, N + i) = 1
VAR(i) = N + i
Next i
For j = 1 To N
MAT(0, j) = -(Sheets("Sheet1").Cells(9, 2 + j).Value)
Next j
'Step0の出力
ITER = 0
OUTPUT
Do While ITER < 50
ITER = ITER + 1
'ピボット列の選定(基底に入れる変数の決定)
Max = 0
PIVOT = 0
For j = 1 To MN
If MAT(0, j) < 0 Then
If MAT(0, j) <= Max Then
PIVOT = j
Max = MAT(0, j)
End If
End If
Next j
If PIVOT = 0 Then Exit Do
'ピボット行の選定(基底から追い出す変数の決定)
Min = 10000000000#
Row = 0
For i = 1 To M
If MAT(i, PIVOT) > 0 Then
DUMMY = MAT(i, 0) / MAT(i, PIVOT)
If DUMMY >= 0 Then
If DUMMY <= Min Then
Row = i
Min = DUMMY
End If
End If
End If
Next i
'基底変数の交換およびピボット演算
DUMMY = MAT(Row, PIVOT)
For j = 0 To MN
MAT(Row, j) = MAT(Row, j) / DUMMY
Next j
For i = 0 To M
If i <> Row Then
DUMMY = MAT(i, PIVOT)
For j = 0 To MN
MAT(i, j) = MAT(i, j) - MAT(Row, j) * DUMMY
Next j
End If
Next i
VAR(Row) = PIVOT
OUTPUT
test = 1
Loop
End Sub
Sub OUTPUT()
Sheets("Sheet1").Cells(18 + 10 * ITER, 1).Formula = "Step" & ITER
Sheets("Sheet1").Cells(19 + 10 * ITER, 1).Formula = "基底変数"
Sheets("Sheet1").Cells(19 + 10 * ITER, 2).Formula = "制限"
For j = 1 To MN
Sheets("Sheet1").Cells(19 + 10 * ITER, j + 2).Formula = "X" & j
Next j
Sheets("Sheet1").Cells(20 + 10 * ITER, 1).Formula = "-Z"
For i = 1 To M
Sheets("Sheet1").Cells(20 + 10 * ITER + i, 1).Formula = "X" & VAR(i)
Next i
For i = 0 To M
For j = 0 To MN
Sheets("Sheet1").Cells(20 + 10 * ITER + i, j + 2).Value = MAT(i, j)
Next j
Next i
End Sub
生産管理は工場にとって、重要テーマであり実用的にはもっと複雑な生産管理システム を導入しているでしょう。
的確な管理を行うには、日々変化する生産状況のデータを自動収集し、最適な生産管理を 行うことが、不可欠でしょう。
シンプレックス法は的確な生産管理システムの道具の一つにすぎません。