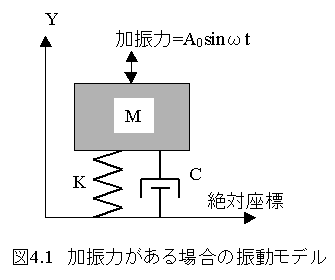
加振力がある場合の振動モデル図4.1に加振力がある場合の振動モデルを示します。
加振力
F=A0sinωt -----（4.1）
が質量Mに加わるとします。
質量MはバネKと粘性抵抗Cで土台（絶対座標）に接しているとします。
質量Mの運動方程式は
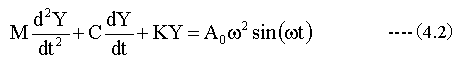
（4.2）式が質量Mの運動方程式です。
この解は
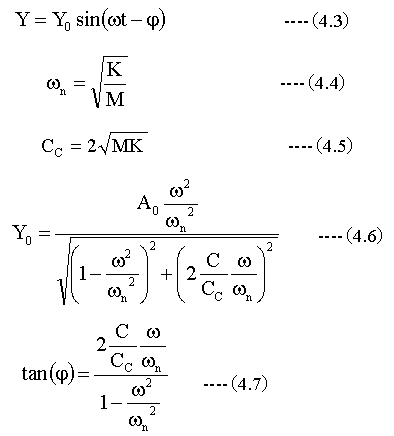
と振動に関する本に書いてありました。
上記の式が正しいか?検証する必要があります。
代入法による微分方程式の解以下の式を微分方程式に代入して微分方程式の解を求めます。
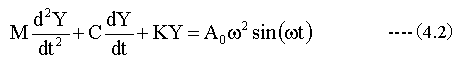
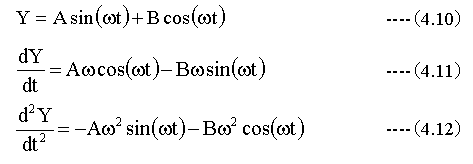
（4.10）、（4.11）、（4.12）式を4.2式に代入して
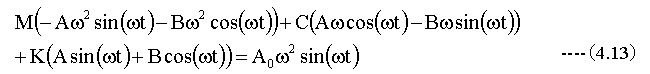
（4.13）式のsin(ωt）、cos(ωt)の係数が左辺、右辺で等しいとおくと
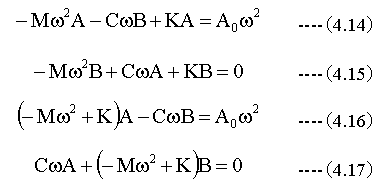
(4.16)(4.17)式から
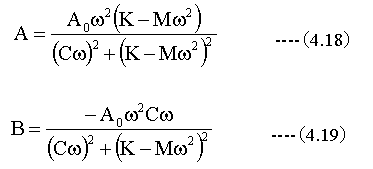
（4.10）式を下記のように書き直すと
上記の結果が得られます。
上記の代入式は、角速度ωの振動成分に着目した特殊解を得る方法です。 角速度ωの振動成分以外は無視されており、正しい一般解ではありません。
代入法で微分方程式の一般解を得るためには、あらかじめ正しい一般解の関数形が わかっていなければなりません。
これが、代入法の欠点です。
ただし、着目した角速度ωの振動成分に関する式を得ることができます。
２章：ラプラス変換法による微分方程式の解に行く。