ラプラス変換法とは？私の個人的な経験ですが、算数・数学に関して、平均してみれば得意科目でしたが、 にがて・スランプの時期もありました。
一番古い記憶でが、算数での九九の暗記に苦労した記憶があります。
例えば3×3＝9の演算ですが、これは3+3+3＝9と同じ意味です。
しかし、掛け算を足し算で行うと時間がかかってしまいます。 したがって、九九は丸暗記しないと時間内に計算問題を解けなくなってしまいます。
最大のスランプは1967年頃学んだ、複素関数論から始まるラプラス変換とラプラス逆変換です。
複素関数に関するさまざまな定理や公式が何の役に立つのか？理解できずスランプに陥りました。
後になって考えるに複素関数論、ラプラス変換、ラプラス逆変換は線形微分方程式を解くための道具、 すなわち計算尺のようなものであることに気づきました。
複素関数に関するさまざまな定理や公式の多くは、ラプラス逆変換の正当性を証明するものとラプラス逆変換 のための道具でした。
全ての定理や公式を証明しようとすると大変難しいのですが、線形微分方程式を解くための道具と 割り切れば、大変便利な道具として活用できます。
ラプラス変換法による微分方程式の解ラプラス変換法で下記の微分方程式を解きます。
質量Mの運動方程式は
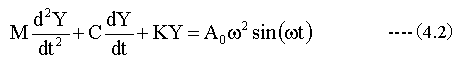
以下のラプラス変換の公式を用います。
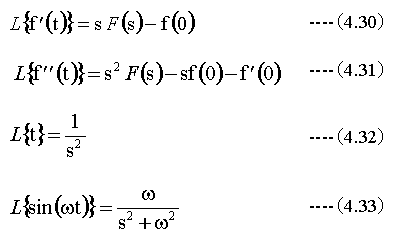
（4.2）式に、初期条件（ｆ（0）=0、f'(0)=0）として、（4.30）〜（4.33）式を代入して整理すると
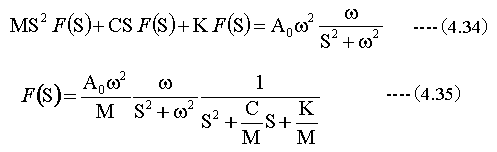
2次方程式の解を用いて（4.35）式の分母を因数分解します。
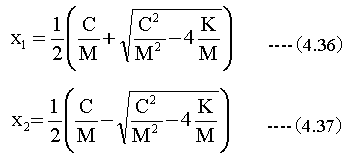
（4.36）（4.37）式を用いて
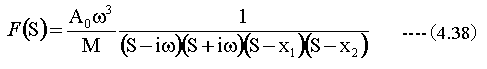
ここで、ラプラス逆変換の定理を使用します。
ラプラス変換の分母Q(s)がすべてあい異なる1次因数s-a1、 s-a2、 s-a3、---- s-an に 分解できれば、以下の式が成立する。
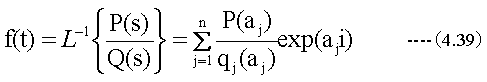
（4.39）式において、ｑj(s)はQ(s)からs-ajを除いた残りの全ての因数の積である。
（4.38）式において
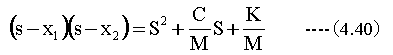
S=iωにおいて
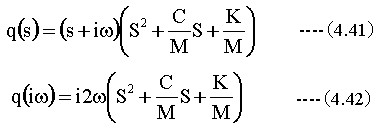
S=-iωにおいて
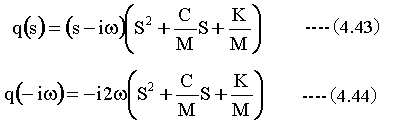
S=ｘ1において
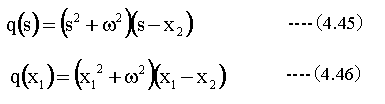
S=ｘ2において
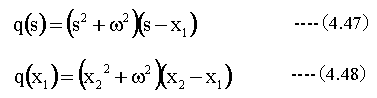
従って（4.38）式の逆変換は
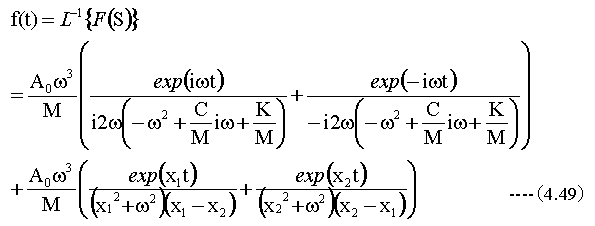
（4.49）式を変形すると
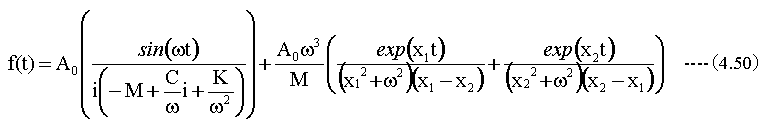
ラプラス変換法による微分方程式解の解釈- ラプラス変換法では正しい微分方程式の一般解が求まります。
- 微分方程式は初期条件をいれて解く必要があります。（ｆ（0）=0、f'(0)=0としました。）
- 解の第1項は角速度ωの単振動です。
- ｘ1とｘ2は複素数となります。従って
- 解の第２項は固有振動数の減衰振動となります。
- 解は複素数の関数となっています。複素関数を使用すれば、
このまま計算できます。（実数計算のための変換は省略します。）
３章：連立ルンゲ・クッタ法による微分方程式の解に行く。