連立ルンゲ・クッタ法とは？私の個人的な経験ですが、ルンゲ・クッタ法は1968年頃学びました。
1967年頃学んだ、ラプラス変換とラプラス逆変換がスランプでしたので画期的な方法と感じました。
1969年には初めてプログラマブル計算機を体験しました。初めて作ったプログラムがルンゲ・クッタ法です。
ルンゲ・クッタ法の理論については
「特設講座」有能エンジニアのための実用数値計算で紹介しています。
N元の連立微分方程式の解まず、N元の連立微分方程式は下記に示す形に変形します。
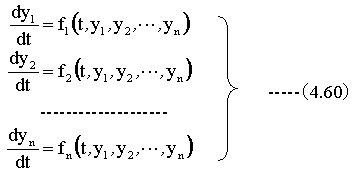
次に初期値を用いて、下記の計算をします。
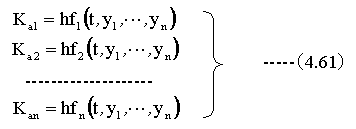
次に下記の計算をします。
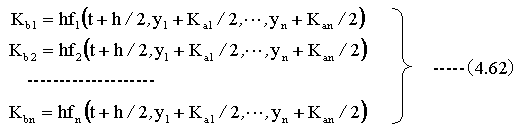
次に下記の計算をします。
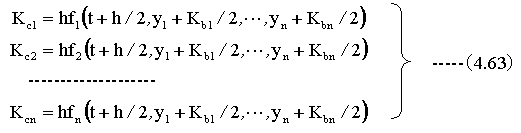
次に下記の計算をします。
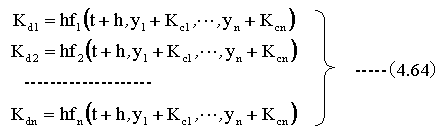
そして、最後に下記の式で初期値+変化幅を計算し、次の変数の値を求めます。
以上の計算操作を繰り返すことにより、N元の連立微分方程式の変数の変化を 次々と求めることができます。
（4.2）式の微分方程式の解（4.2）式の微分方程式を以下に示します。
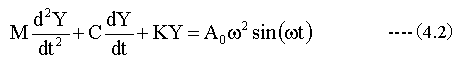
N元の連立微分方程式にあてはめるため、下記式のように変形します。
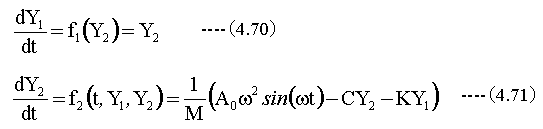
(4.70)式と（4.71）式をN元の連立微分方程式にあてはめると以下のようになります。
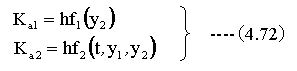
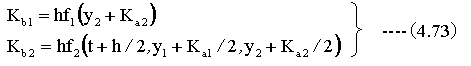
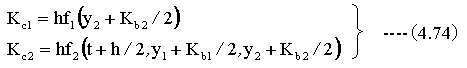
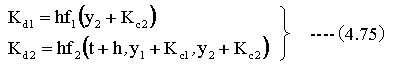
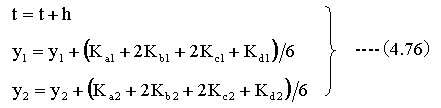
以上の計算を繰り返すことにより、微分方程式の解を求めることができます。
以上のような単純計算を繰り返すことにより、微分方程式の解が求まるのはマジック のようですが、確認は実際に計算してみるのが一番です。