フーリエ変換一般式フーリエ変換一般式を下記に示します。
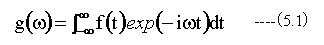
また、フーリエ逆変換は
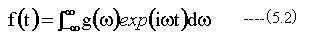
離散的フーリエ変換N個のデータｆ(k)(k=0〜N-1）が与えられた時、N個の有限列G(n)をf(k)の離散的フーリエ変換といい次式によって定義される。
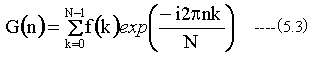
また、フーリエ逆変換は
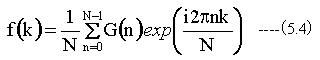
（5.4）式正規化定数1/Nは(5.3)式と(5.4)式のどちらかにいれる。または平方根にして両方にいれて良い。
高速フーリエ変換（5.3）式をつぎのように書く
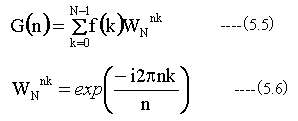
N=2、すなわちデータ数が2個の場合（5.5）式は以下のようになる。
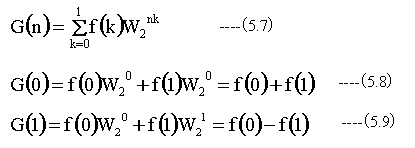
(5.7)式の演算においては、指数の項が消えて単純な和と差の項のみが残ります。
これが、データ数N=2の場合のフーリエ変換の重要な特徴であり、演算時間の短縮を可能としています。
また、（5.6）式のWNを回転子と呼びます。
データ数N=8の場合の高速フーリエ変換データ数がN=8の場合について考えてみます。 （5.5）式は以下のようになります。
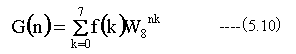
ここで、nとkを2進数に分解します。
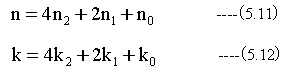
そして(5.10)式を以下のように変形します。
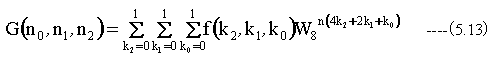
（5.13）式の右辺の和を外側から計算を実行します。
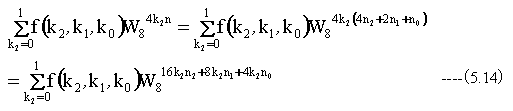
ここで
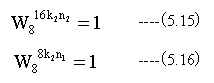
ゆえに
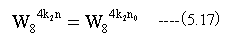
回転子の定義から
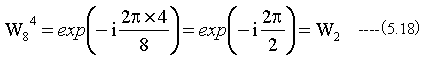
したがって
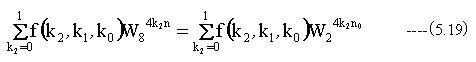
となります。これはN=2のDFTそのものです。
(5.13)式に(5.19)式を代入して
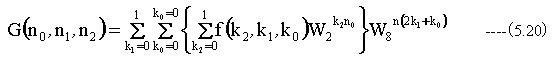
(5.20)式を得ます。 { }の中のDTFをG1(n0,k1,k0)とおき、k1について整理すると
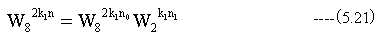
（5.21）式より
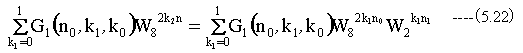
(5.22)式を得ます。これは、 G1(n0,k1,k0)に回転子W82k1n0をかけたものに対するN=2のDTFになっています。
(5.22)式を（5.20）式に代入して
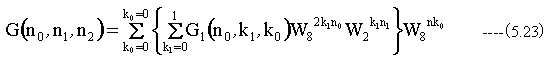
(5.23)式を得ます。ふたたび{ }の中のDTFをG2(n0,n1,k0)とおき、また
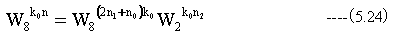
（5.24）式より
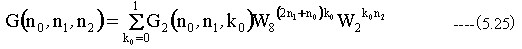
データ数N=16の場合の高速フーリエ変換N＝16のFFTの演算はさらに複雑になります。実用的にはNの数を大きく 設定する必要があります。
FFTをDFTに分解するには、
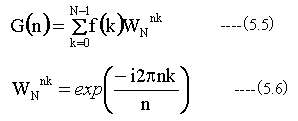
(5.5)式において、WNnkがどのように分解されるかを調べればよいのです。
いきなりNの数を一般化するのは飛躍を伴いますので、N=16のFFTについて検討します。
（5.26）式の性質を利用します。また、
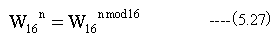
(5.27)式を用いて整理します。Nとkを2進数で表して
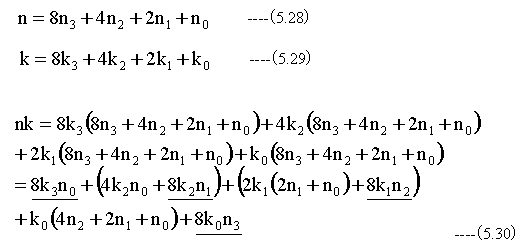
(5.30)式において、アンダーバーの部分は下記ようにN=2のDFTに置き換えることができます。
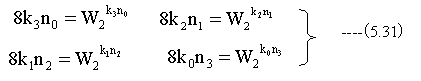
残りの項は途中の結果に掛け合わされる回転子となります。
ここで、データ数NとDFT演算の段(m)とN=2のDFT演算子(kn)と回転子(arg)の関係を整理 してみましょう。
高速フーリエ変換の回転子表高速フーリエ変換の回転子を整理すると以下の表になります。
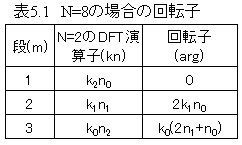
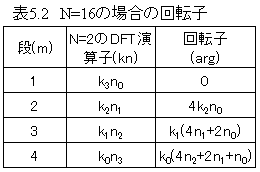
高速フーリエ変換の回転子の規則性上記表から回転子の規則性を見出します。
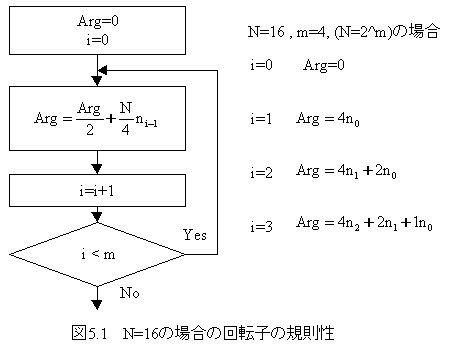
上記の規則性を利用すれば、より大きなデータ数Nに対するFFTが可能です。
２章：プログラミングの課題に行く。