虚数（i）の定義
（1.1）式の解について考えてみましょう！！
実数だけで考えると（1.1）式の解は無いことになります。こんな簡単な方程式でも、実数だけでは解を得ることができません。
どうすれば、 （1.1）式の解を得ることができるでしょうか？
自乗して-1になる数の虚数（i）を定義すれば、 （1.1）式の解を得ることができます。しかし、虚数（i）が何を意味するか？理解するのは、難しいものがあります。
しかし、虚数（i）を定義しなければ、多くの方程式は解無しということになります。いやがおうにも虚数（i）を使用せざるえないことが多々生じます。
それならば、虚数（i）の定義を認め、虚数（i）の性質を調べた方が賢いのです。そして、虚数（i）の定義を認めることにより、さまざまな方程式の解を得ることができます。
複素数の定義
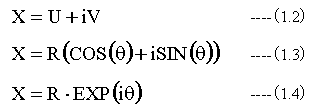
複素数とは実数と虚数のペアとして定義されます。定義式としては、(1.2)式、 (1.3)式、 (1.4)式の形式で表すことができますが、 (1.4)式の形式が比較的に多く使用されます。
複素関数グラフのワークブック「複素関数1.xls」のダウンロード下記のワークブック「複素関数1.xls」をダウンロードしてください。
ダウンロード後はダブルクリックで解凍してから使用してください。
ワークブック「f21-1.xls」をダウンロードする。ワークブック「複素関数1.xls」説明- ワークブック「複素関数1.xls」は複素関数機能を使用しています。
- 複素関数機能を使うには、メニューの「ツール(T)」＿「アドイン(I)」を選択し、アドインリストの「分析ツール」にチェックマークを設定する必要があります。
- シート「Y=X^2+1」はY=X^2+1の関数グラフです。
- シート「Y=X^3+1」はY=X^3+1の関数グラフです。
- シート「Y=X^4+1」はY=X^4+1の関数グラフです。
シート「Y=X^2+1」シート「Y=X^2+1」には、下記のグラフが表示されています。
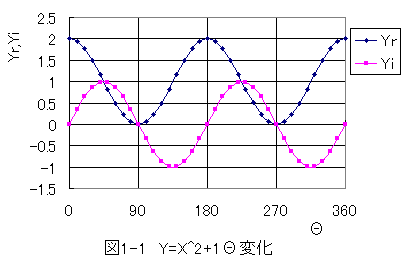
図1-1において、Yrが実数、Yiが虚数です。
Θ＝90度とΘ＝270度の位置でYr＝0、Yi＝0を満足します。
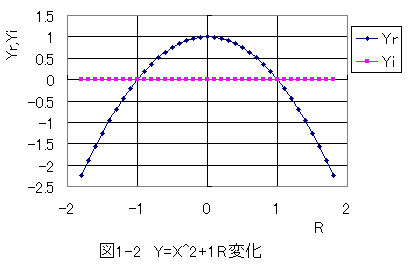
図1-2はΘ＝90度の位置でRを変化させたグラフです。
Yrだけが変化し、Yiが変化しないことがわかります。
シート「Y=X^3+1」シート「Y=X^3+1」には、下記のグラフが表示されています。
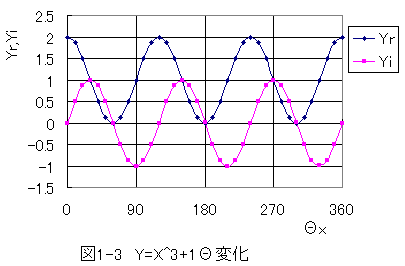
図1-3において、Yrが実数、Yiが虚数です。
Θ＝60度とΘ＝180度とΘ＝300度の位置でYr＝0、Yi＝0を満足します。
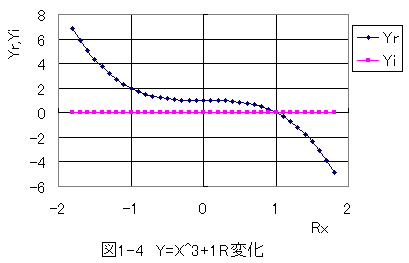
図1-4はΘ＝60度の位置でRを変化させたグラフです。
Yrだけが変化し、Yiが変化しないことがわかります。
シート「Y=X^4+1」シート「Y=X^4+1」には、下記のグラフが表示されています。
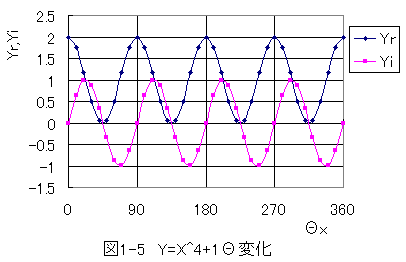
図1-5において、Yrが実数、Yiが虚数です。
Θ＝45度とΘ＝135度とΘ＝225度とΘ＝3155度の位置でYr＝0、Yi＝0を満足します。
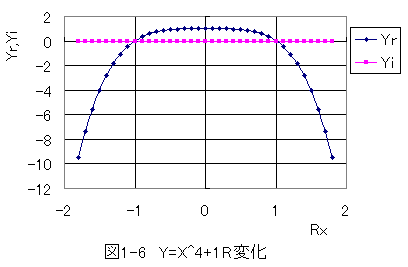
図1-6はΘ＝45度の位置でRを変化させたグラフです。
Yrだけが変化し、Yiが変化しないことがわかります。
累乗関数の性質方程式 （X^n）+1=0 を満足する解はｎ個存在することがわかります。
上記の方程式は実数のみで考えると解がありませんが、複素数を定義すること により、解が得られることがわかりました。
では、もっと一般的な高次の方程式の解はもとまるでしょうか？
結論から言うとｎ次の高次方程式の解はｎ個求めることができます。
しかし、一般的な高次の方程式の解を求めるには複雑な計算を必要とします。 一般的な高次の方程式の解を求め方は次章で説明します。
２章：高次方程式解の求め方に行く。