２元ニュートン法高次方程式の解を求めるため、 ２元ニュートン法を用います。
高次方程式を下記のように記述します。
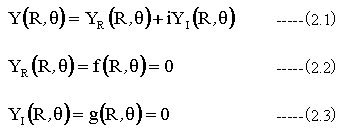
(2.2)式と（2.3）式を（R,θ）のまわりで展開し、Rとθの変化量をそれぞれ（ΔR、Δθ）とすると
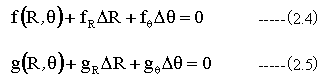
（2.4）式と（2.5）式を解いて
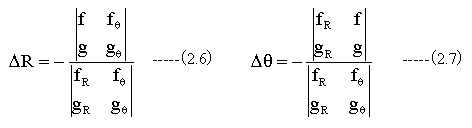
次のRとθの値を下記式で求めます。
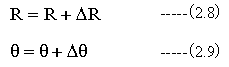
（2.6）式から（2.9）式の計算を繰り返すことにより、 Rとθの値は方程式の解に収束します。
上記の計算は関数形を限定しておらず、任意の形式の方程式の解に収束します。解が多数個ある場合はどこかの解に収束しますが一般的に計算をスタートしたRとθの値に近い点に収束します。
6次方程式の全ての解をもとめる一例になりますが6次方程式の全ての解を求めてみたいと思います。
上記の2元ニュートン法で1個の解X=Cが求まったとします。
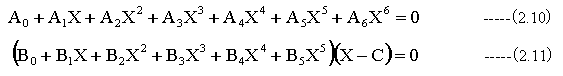
（2.10）式は6次方程式の一般形です。A0〜A6は任意の複素数の定数です。
X=Cは（2.10）式の1個の解であり、（2.11）式のように変形できます。
（2.10）式と（2.11）式の定数を比較することにより下記の関係式が得られます。
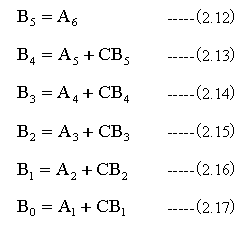
(2.12)式〜（2.17）式により、 6次方程式が5次方程式に変えることができます。
同様な操作を繰り返すことにより、6個の解全てを求めることができます。
３章：高次方程式のフリープログラムに行く。