複素関数の定積分複素関数も実数の関数と全く同様に定積分することが可能です。
しかし、複素関数の定積分は実数の場合とちょっと異なる要素が加わってきます。
一般に関数F(X)の微分関数がｆ（X)であるとき、F(X)をｆ（X)の原始関数といいます。
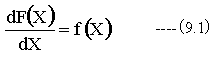
実数の定積分G(a,b)は下記式で定義されます。
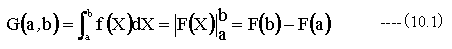
（10.1）式において、aとｂは定数です。
複素関数の定積分はどうなるでしょうか？複素関数の場合はXが複素数の変数、ｄXが複素数の微小量、aとbが複素数の定数とすればよいのです。
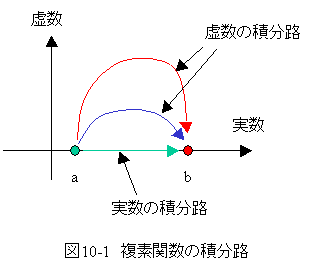
複素関数の積分路さて、定積分の積分路をどうなるでしょうか？
実数の場合の積分路は一義的に定まりますが、複素数の場合は、無限に積分路を選択できます。
（10.1）式の定義からわかるように、積分の結果はaとbの値のみできまり、積分路には依存しません。
なぜ？こうなるのか？不思議な気もしますが、関数ｆ（X)の原始関数F(X)が存在する場合は、 (10.1）式の定義から明らかです。
関数ｆ（X)に特異点（極）が存在する場合は、積分路により、値がことなります。
複素関数グラフのワークブック「複素関数10.xls」のダウンロード下記のワークブック「複素関数10.xls」をダウンロードしてください。
ダウンロード後はダブルクリックで解凍してから使用してください。
ワークブック「複素関数10.xls」をダウンロードする。ワークブック「複素関数10.xls」説明- ワークブック「複素関数10.xls」は複素関数機能を使用しています。
- 複素関数機能を使うには、メニューの「ツール(T)」＿「アドイン(I)」を選択し、アドインリストの「分析ツール」にチェックマークを設定する必要があります。
- 「複素関数10.xls」をダブルクリックで起動します。
（マクロを有効にして開いてください！！）
- シート「操作」はパラメータの設定と操作を行います。
- シート「OUT_FM」は数値積分の計算結果です。
- シート「Graph1」は計算結果のグラフです。
シート「操作」- 定数 A：Y=A*X^2の定数を設定します。
- X^2 X^2：=IMPOWER(C9,2)を設定します。
- Xr(0) ：積分路スタート点の実数を設定します。
- Xi(0) ：積分路スタート点の虚数を設定します。
- Xr(1) ：積分路1本目の終点の実数を設定します。
- Xi(1) ：積分路1本目の終点の実数を設定します。
- N（1） ：積分路1本目の分割数を設定します。
- Xr(2) ：積分路2本目の終点の実数を設定します。
- Xi(2) ：積分路2本目の終点の実数を設定します。
- N（2） ：積分路2本目の分割数を設定します。
- Xr(3) ：積分路3本目の終点の実数を設定します。
- Xi(3) ：積分路3本目の終点の実数を設定します。
- N（3） ：積分路3本目の分割数を設定します。
- Xr(4) ：積分路4本目の終点の実数を設定します。
- Xi(4) ：積分路4本目の終点の実数を設定します。
- N（4） ：積分路4本目の分割数を設定します。
注（１）積分路は斜め線の設定も可能です。
注（２）積分路数の最大は50本です。
- 「計算実行」ボタンを押すと計算を実行します。
複素関数Y=3*X^2の定積分の検証複素関数Y=3*X^2の積分はX^3となります。この条件において 数値積分を行った結果を図10-2に示します。
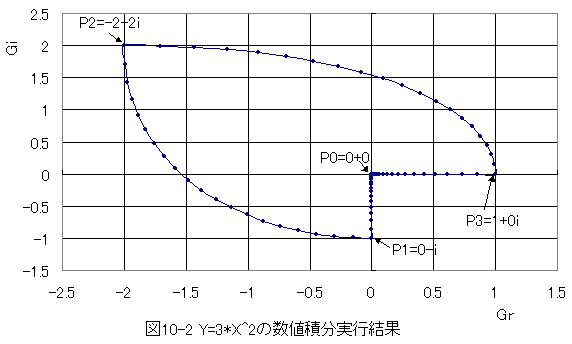
- P0点：積分開始点であり当然値はゼロとなります。
- P1点の（10.1）式での計算結果は以下となります。
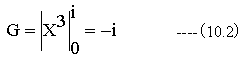
- P2点の（10.1）式での計算結果は以下となります。
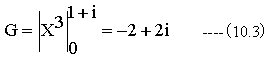
- P3点の（10.1）式での計算結果は以下となります。
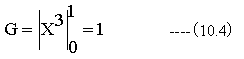
- 一周して元の位置に戻ると数値積分の結果はゼロとなります。
複素関数Y=3*X^2の定積分の検証結果まとめ- 数値積分の結果と（10.1）式での計算結果はほぼ完全に一致します。
- 特異点（極）のない関数の積分は（10.1）式で簡単に計算できます。
- 積分値は積分路によって変化しない、すなわち始点と終点できまる。
１１章：特異点（極）のある複素関数の定積分に行く。