コーシーの積分表示コーシーの定理の中でもコーシーの積分表示として知られる以下の定理は重要です。
「コーシーの積分表示定理」ｆ（X)が単一連結領域Dの境界C上およびその内部で解析的ならば、D内の任意の1点aにおける値は
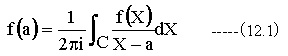
となります。
さて、（12.1）式が何故重要なのでしょうか？それは、 （12.1）式がラプラス逆変換と等価の積分となっているためです。ラプラス変換とラプラス逆変換は高次の微分方程式を解析的に解く手段として優れています。
言い換えると（12..1）式は高次の微分方程式を解析的に解く手段として重要です。
ラプラス逆変換ラプラス逆変換はSと時間ｔを変数として以下の式となります。
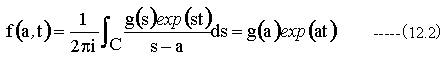
(12.2)式の変数sをXに置き換えると（12.1）式と同じ積分形となり、ラプラス逆変換の解析解が求まります。
従って、 （12.1）式はラプラス逆変換を行うにあたって、重要な公式となります。
（12.1）式の証明積分路は点aを中心とした微小半径ｒの円形で積分します。
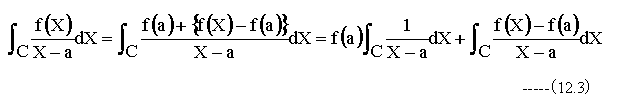
ここで
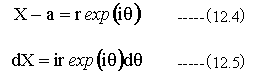
(12.3)式の第1項に(12.4)式、(12.5)式を代入して
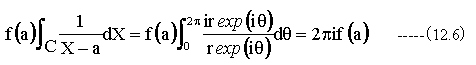
次に(12.3)式の第2項がｒを小さくするとゼロに近づくことを証明すればよい。
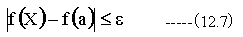
とするならば
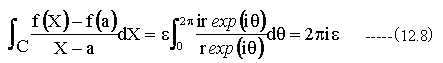
ここでｒ→0とするならば、ε →0となる。
従って(12.6)式と(12.3)式から
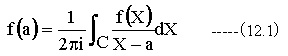
となります。
数値積分による検証下記の式を数値積分の結果と比較して見たいと思います。
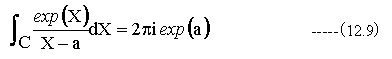
まず、下記の式を数値積分します。
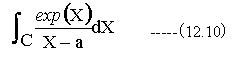
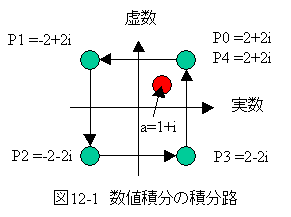
積分路は図12-1に示す積分路とします。
また、a=1+iとします。
複素関数グラフのワークブック「複素関数12.xls」のダウンロード下記のワークブック「複素関数12.xls」をダウンロードしてください。
ダウンロード後はダブルクリックで解凍してから使用してください。
ワークブック「複素関数12.xls」をダウンロードする。ワークブック「複素関数12.xls」説明- ワークブック「複素関数10.xls」は複素関数機能を使用しています。
- 複素関数機能を使うには、メニューの「ツール(T)」＿「アドイン(I)」を選択し、アドインリストの「分析ツール」にチェックマークを設定する必要があります。
- 「複素関数10.xls」をダブルクリックで起動します。
（マクロを有効にして開いてください！！）
- シート「操作」はパラメータの設定と操作を行います。
- シート「OUT_FM」は数値積分の計算結果です。
- シート「Graph1」は計算結果のグラフです。
シート「操作」- 定数 a：Y＝exp(X)/(X-a)の定数を設定します。
- X-a X-a：=IMSUB(C9,C13)を設定します。
- exp(X) exp(X)：=IMEXP(C9)を設定します。
- 積分路数 Nr：積分路数を設定します。
- Xr(0) ：積分路スタート点の実数を設定します。
- Xi(0) ：積分路スタート点の虚数を設定します。
- Xr(1) ：積分路1本目の終点の実数を設定します。
- Xi(1) ：積分路1本目の終点の実数を設定します。
- N（1） ：積分路1本目の分割数を設定します。
- Xr(2) ：積分路2本目の終点の実数を設定します。
- Xi(2) ：積分路2本目の終点の実数を設定します。
- N（2） ：積分路2本目の分割数を設定します。
- Xr(3) ：積分路3本目の終点の実数を設定します。
- Xi(3) ：積分路3本目の終点の実数を設定します。
- N（3） ：積分路3本目の分割数を設定します。
- Xr(4) ：積分路4本目の終点の実数を設定します。
- Xi(4) ：積分路4本目の終点の実数を設定します。
- N（4） ：積分路4本目の分割数を設定します。
注（１）積分路は斜め線の設定も可能です。
注（２）積分路数の最大は50本です。
- 「計算実行」ボタンを押すと計算を実行します。
複素積分（12.10）式の数値計算結果数値積分を行った結果を図11-2に示します。
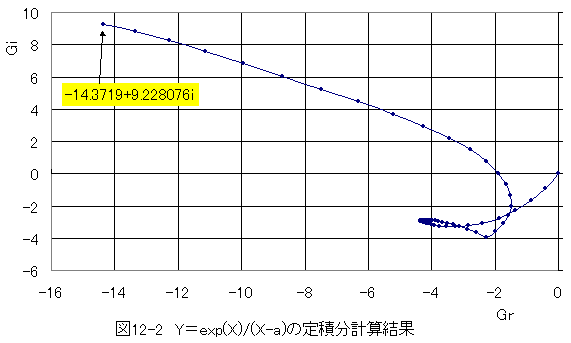
複素積分（12.9）式の代数計算結果コーシーの積分表示で代数的に計算した結果を下記に示します。
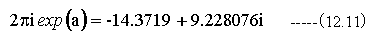
複素関数Y=3*X^2の定積分の検証結果まとめ- 数値積分の結果とコーシーの積分表示で代数的に計算した結果は完全に一致します。
- 積分路は特異点（極）を含む閉曲線であれば、計算結果は同じとなります。
- 積分路の回転方向を逆にすると符号が反転します。
- 積分路が２周すると、積分値が倍になります。
１３章：コーシーの係数公式に行く。