ラプラス変換の定義式ラプラス変換は時間ｔの関数ｆ（ｔ）に対して、任意の複素数変数ｓに関して下記のように定義される
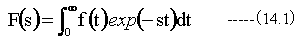
ラプラス逆変換の定義式ラプラス逆変換は複素変数sの関数F(s)に関して下記のように定義される。
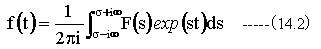
定義式の正当性(14.1)式と(14.2)式は変数変換の式であるが、なぜ？この様な複雑な演算を行う必要があるのか？疑問を持たれると思います。
(14.1)式においては、関数f(t)に関数exp(st)をかけてｔについて積分しています。ここで積分公式
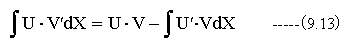
を使用してV’=f’(t),U＝exp(-st)とおくならば、V=f(t)、U’＝ -sexp(-st)となり、（14.1）式は以下のように変形できます。
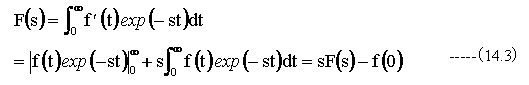
(14.3)式の例に示すように、exp(-st)は、微分しても関数の形が変わらないため、代数的な積分がやりやすいという特徴があります。
この性質を利用して、さまざまなラプラス変換の公式が証明できます。
次に（14.2）式のラプラス逆変換の式ですが直感的には、なぜこの計算で逆変換できるのかが理解できません。
また、 （14.2）式の積分はコーシーの積分表示と等価です。
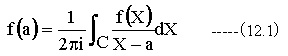
複素変数の積分は積分路を自由に選択することができます。 （14.2）式の積分路σ-i∞〜 σ+i∞は（12.1）式の積分路Cと等価なのです。
全ての特異点(極）を含む閉曲線を選択すれば、積分路σ-i∞〜 σ+i∞と等価となります。従って、 （12.1）式を用いて、代数的に逆変換を実行できる訳です。
ラプラス逆変換の定義式の正当性については、うまく説明できませんが、幾つかの事例について、検証を行ってみたいと思います。
１５章：ステップ関数のラプラス変換に行く。