1次関数のラプラス変換t > 0 において
f(t)=t の時
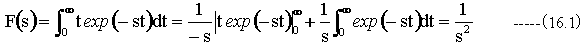
1次関数のラプラス逆変換コーシーの係数公式（13.2）式を変形します。
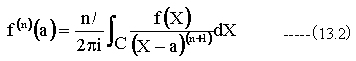
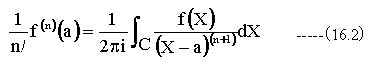
ゆえに
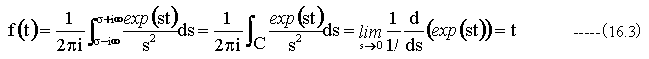
２次関数のラプラス変換t > 0 において
f(t)=t＾2 の時
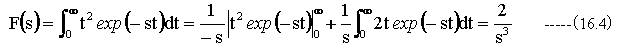
２次関数のラプラス逆変換逆変換は同様に（16.2）式を使用します。
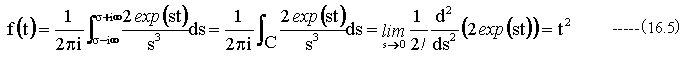
となり、ラプラス逆変換を行うと完全に元の関数形に戻ります。
一見、トリックを使っているようにも思われます。
数値計算による検証数値計算を用いれば、コーシーの係数公式を用いることなく、ラプラス逆変換の定義式のまま計算できます。
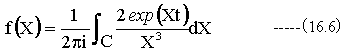
（16.5）式の数値計算を実行します。
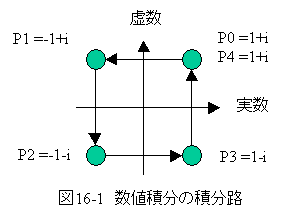
閉曲線の積分路は、図16-1に示す通りとします。
時間ｔは0〜5までを10分割して計算するとします。
複素関数グラフのワークブック「複素関数16.xls」のダウンロード下記のワークブック「複素関数16.xls」（ラプラス逆変換プログラム）をダウンロードしてください。
ダウンロード後はダブルクリックで解凍してから使用してください。
ワークブック「複素関数16.xls」をダウンロードする。ワークブック「複素関数16.xls」説明- ワークブック「複素関数16.xls」は複素関数機能を使用しています。
- 複素関数機能を使うには、メニューの「ツール(T)」＿「アドイン(I)」を選択し、アドインリストの「分析ツール」にチェックマークを設定する必要があります。
- 「複素関数16.xls」をダブルクリックで起動します。
（マクロを有効にして開いてください！！）
- シート「操作」はパラメータの設定と操作を行います。
- シート「OUT_FM」は数値積分の計算結果です。
- シート「Graph1」は計算結果のグラフです。
シート「操作」- 定数 A：Y＝A*exp(Xｔ)/X^3の定数(=2)を設定します。
- Xt Xt：=IMPRODUCT(C9,C13)を設定します。
- X^3 (X^3)：=IMPOWER(C9,3)を設定します。
- exp(Xt) ：=IMEXP(C14)を設定します。
- 初期時間 ts：初期時間を設定します。
- 終了時間 te：終了時間を設定します。
- 時間分割数 Nt：時間分割数を設定します。
- 積分路数 Nr：積分路数を設定します。
- Xr(0) ：積分路スタート点の実数を設定します。
- Xi(0) ：積分路スタート点の虚数を設定します。
- Xr(1) ：積分路1本目の終点の実数を設定します。
- Xi(1) ：積分路1本目の終点の実数を設定します。
- N（1） ：積分路1本目の分割数を設定します。
- Xr(2) ：積分路2本目の終点の実数を設定します。
- Xi(2) ：積分路2本目の終点の実数を設定します。
- N（2） ：積分路2本目の分割数を設定します。
- Xr(3) ：積分路3本目の終点の実数を設定します。
- Xi(3) ：積分路3本目の終点の実数を設定します。
- N（3） ：積分路3本目の分割数を設定します。
- Xr(4) ：積分路4本目の終点の実数を設定します。
- Xi(4) ：積分路4本目の終点の実数を設定します。
- N（4） ：積分路4本目の分割数を設定します。
注（１）積分路は斜め線の設定も可能です。
注（２）積分路数の最大は50本です。
- 「計算実行」ボタンを押すと計算を実行します。
ラプラス逆変換（16.5）式の数値計算結果ラプラス逆変換を行った結果の実数部を図16-2に示します。
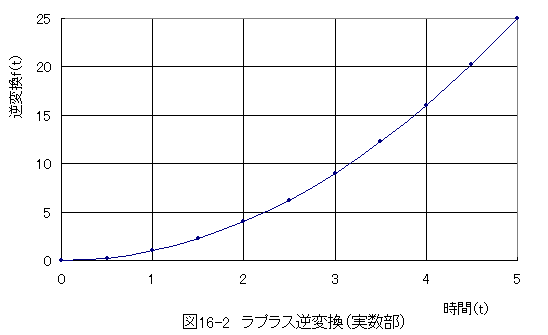
ラプラス逆変換を行った結果の虚数部を図16-2に示します。
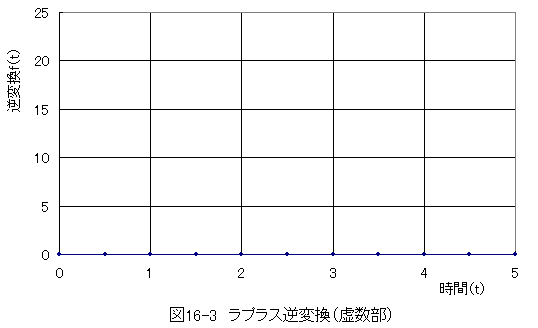
ラプラス逆変換の数値計算の結果と代数解は完全に一致します。
１７章：exp・sin関数のラプラス変換に行く。