指数関数のラプラス変換t > 0 において
f(t)=exp(kt) の時（kは定数）
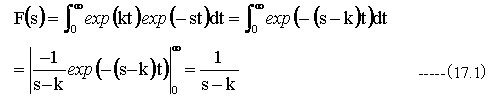
指数関数のラプラス逆変換逆変換はコーシーの積分表示（12.1）式から
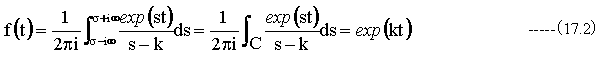
となり、逆変換により完全に元の関数形に一致します。
sin関数のラプラス変換t > 0 において
f(t)=sin(t) の時
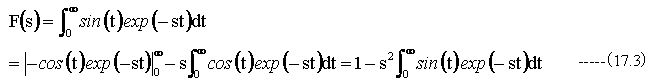
ゆえに
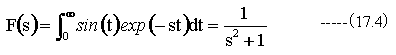
sin関数のラプラス逆変換逆変換はコーシーの積分表示（12.1）式から
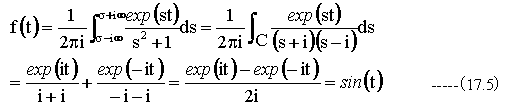
となり、逆変換により完全に元の関数形に一致します。
ラプラス変換後の関数形において、分母が1次の特異点(極）に分解できるとき、逆変換にコーシーの積分表示（12.1）式を適用でき、逆変換後の関数形は元の関数形と完全一致します。
ラプラス変換後の関数形において、分母が2次以上の特異点(極）を持つ場合は、exp(st)の級数展開が必要となります。
ラプラス逆変換の定義式
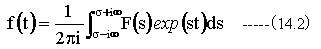
（14.2）式は、以上の逆変換操作において矛盾が生じていないことが確認できます。
１８章：ラプラス逆変換の基本テクニックに行く。