導関数（微分関数）のラプラス変換ラプラス変換・ラプラス逆変換の最大の応用は、微分方程式への応用です。その前に導関数（微分関数）のラプラス変換を復習したいと思います。
ラプラス変換の定義式は
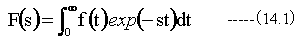
ここでは、下記式のラプラス変換を行います。
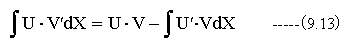
（9.13）式を使用してV’=f’(t),U＝exp(-st)とおくならば、V=f(t)、U’＝ -sexp(-st)となり、（19.1）式は以下のように変形できます。
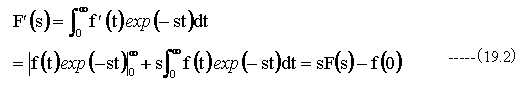
ここで、F(s)は（14.1）式とします。
2階微分関数ｆ’’(t)のラプラス変換次に2階微分関数ｆ’’(t)のラプラス変換を行います。
（9.13）式を使用してV’=f’’(t),U＝exp(-st)とおくならば、V=f’(t)、U’＝ -sexp(-st)となります。
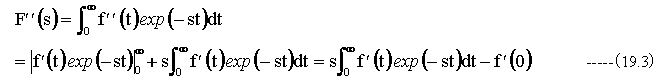
（19.3）式に（19.2）式を代入して
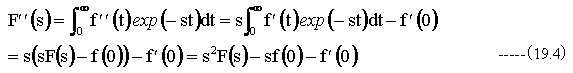
n階微分関数ｆ(n)(t)のラプラス変換上記の操作を繰り返すことにより、 n階微分関数ｆ(n)(t)のラプラス変換式を得ることができます。
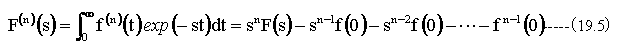
上記の公式は、微分方程式への応用で頻繁に使用されます。
２０章：微分方程式への応用（１）に行く。