常微分方程式への応用ラプラス変換・ラプラス逆変換の最も重要な応用は微分方程式の解法であす。
以下の微分方程式の解を求めます。
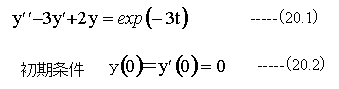
（20.1）式の右辺のラプラス変換は
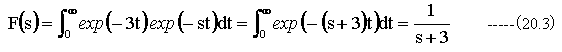
従って、（20.1）式全体をラプラス変換すると
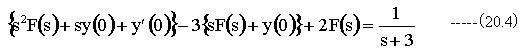
（20.4）式に(20.2)式の初期条件を代入して整理すると
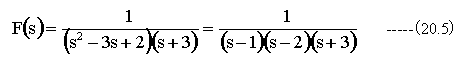
(20.5)式をラプラス逆変換します。
ここで以下の計算を実施します。
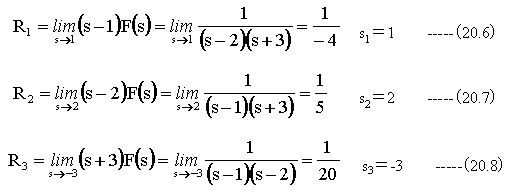
そして
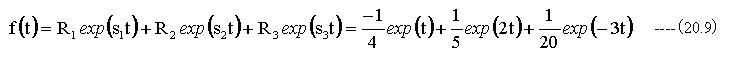
（20.9）式が（20.1）式の解となります。
以上の方法でほとんどの常微分方程式の解を求めることができます。
数値計算による代数解の検証数値計算（ルンゲ・クッタ法）による代数解の検証を行います。
複素関数グラフのワークブック「複素関数20.xls」のダウンロード下記のワークブック「複素関数20.xls」（ラプラス逆変換プログラム）をダウンロードしてください。
ダウンロード後はダブルクリックで解凍してから使用してください。
ワークブック「複素関数20.xls」をダウンロードする。ワークブック「複素関数20.xls」説明- ワークブック「複素関数20.xls」は複素関数機能を使用していません。
- 「複素関数20.zip」をダブルクリックで起動します。
（マクロを有効にして開いてください！！）
- シート「Sheet1」はパラメータの設定と操作を行います。
- シート「比較」は数値積分と代数解の比較です。
- シート「Graph1」はシート「比較」のグラフです。
シート「Sheet1」- 連立数(n) ：2を設定します。
- 時間刻み(h)：0.01を設定します。
- 計算回数(Nc)：200を設定します。
- ｆ1 ：=F12を設定します。
- ｆ2 ：=3*F12-2*F11+EXP(-3*F10)を設定します。
- ｔ（ 0 ） ：0を設定します。
- ｙ1（ 0 ） ：0を設定します。
- ｙ2（ 0 ） ：0を設定します。
- 「計算実行」ボタンを押すと計算を実行します。
数値計算による代数解の検証結果数値計算結果と代数解の比較を図20-1に示します。
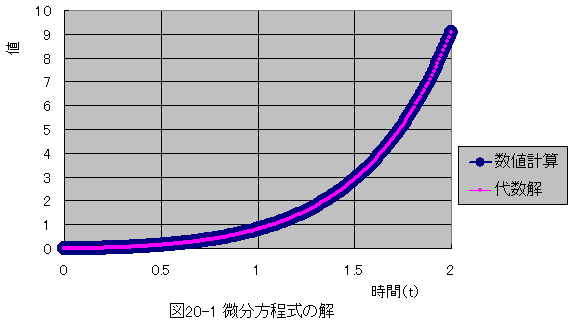
数値計算の結果と代数解は完全に一致します。
２１章：微分方程式への応用（２）に行く。