複素関数の微分の定義複素関数も実数の関数と全く同様に微分することが可能です。
ここでは、変数を以下のように定義します。
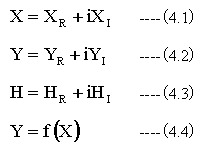
複素関数Yの微分を以下のように定義します。
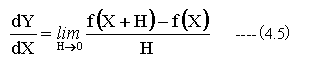
（4.5）式において、X、Y、Hを実数とすれば、実数の微分の定義と一致します。
複素関数Y=X^2の微分複素関数
について検討します。
(4.6)式を（4.5）式に代入します。
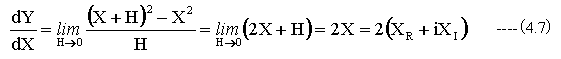
（4.7）式が複素関数Y=X^2の微分です。トリックのように思われますが、各変数を実数部と虚数部に分けて（4.5）式に代入し、整理しても全く同様な結果となります。
従って、実数の関数で得られた微分公式は複素関数にも適用できます。主な公式を下記に示します。
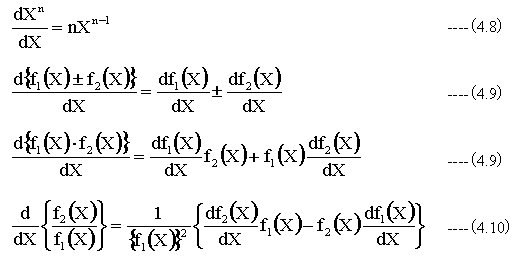
(4.8)式〜（4.10）式以外の三角関数、指数関数、対数関数についても同様に実数の微分公式が複素関数に適用できます。
また、不定積分は微分の逆であることから、実数の不定積分の公式が複素関数に適用できます。
見事なまでに、実数での公式が複素関数に適用できる訳です。数式の変形だけをみているとまるでトリックをみているようです。
本当なのか?実感できる形で確認するには、EXCELで計算しグラフで表してみる必要があります。
５章：EXCELによる累乗複素関数の検証に行く。